| |
Inicio
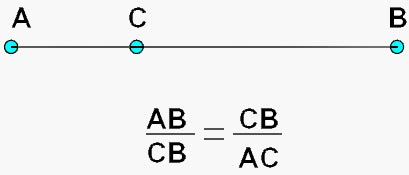
FIG.
1: Relación de proporciones para derivar
el valor del número
La geometría es una de las áreas
matemáticas más empleadas en nuestra
civilización. Desde el tiempo de los egipcios,
muchas construcciones fueron creadas con base
en relaciones geométricas que los científicos
de la época fueron capaces de desarrollar.
Uno de los grandes hallazgos de esa época
es el denominado número de oro o número
áureo (golden number en inglés)
[1-5]. Desde su determinación, han aparecido
de este número muchas demostraciones.
En
este artículo discutiremos algunas de ellas,
especialmente, dentro del ámbito de la física.
Presentaremos también ejemplos en la biología,
anatomía, arquitectura, etc. Más que
tratar de convencer al lector de la importancia
de este número, queremos enfatizar la aparición
de éste en muchos eventos de la naturaleza.
Dejando como cuestión fundamental si la naturaleza
ha sido capaz de desarrollar una relación
universal contenida en este número que pueda
convertirse en una herramienta más en nuestro
análisis para tratar de comprenderla.
El
número áureo, denotado también
como  ,
tiene un valor de (1 + ,
tiene un valor de (1 +  5)
/2. Su nombre se ha propuesto en base a las iniciales
de Pheidias, escultor griego, que supuestamente
usó este número al construir el Partenón
(durante el Renacimiento también se denominó
a este número como la divina proporción). 5)
/2. Su nombre se ha propuesto en base a las iniciales
de Pheidias, escultor griego, que supuestamente
usó este número al construir el Partenón
(durante el Renacimiento también se denominó
a este número como la divina proporción).
Aunque no existe todavía un acuerdo sobre
si  aparece
directamente dentro de las escalas fundamentales
del Partenón, se sabe que aparece claramente
en otras construcciones griegas (teatro Epidaurus,
el teatro de Dionysus en Atenas, etc.) Algunas evidencias
indican que los egipcios usaron esta proporción
para sus construcciones, principalmente, en las
pirámides, pero fue el matemático
Euclides el que encontró una relación
matemática fundamental para derivar su valor.
En la proposición 30, de su libro 5, expone
la siguiente construcción que representamos
en la Fig. 1. Si denominamos como 1 a la longitud
del segmento AB y como x al segmento AC, es fácil
probar que la proporción entre el segmento
largo, al segmento inmediatamente más corto,
da lugar a la ecuación de segundo orden x2
- x + 1, que tiene como solución al número aparece
directamente dentro de las escalas fundamentales
del Partenón, se sabe que aparece claramente
en otras construcciones griegas (teatro Epidaurus,
el teatro de Dionysus en Atenas, etc.) Algunas evidencias
indican que los egipcios usaron esta proporción
para sus construcciones, principalmente, en las
pirámides, pero fue el matemático
Euclides el que encontró una relación
matemática fundamental para derivar su valor.
En la proposición 30, de su libro 5, expone
la siguiente construcción que representamos
en la Fig. 1. Si denominamos como 1 a la longitud
del segmento AB y como x al segmento AC, es fácil
probar que la proporción entre el segmento
largo, al segmento inmediatamente más corto,
da lugar a la ecuación de segundo orden x2
- x + 1, que tiene como solución al número
 . .

FIG.
2: Diferentes tipos de flores que en el
número de sus pétalos dan
lugar a la serie de Fibonacci.
|
Esta
proporción divide a un segmento en
dos, uno más grande que el otro, dando
lugar a un único valor. Esta relación
se ha determinado en diferentes áreas
de la ciencia como una manifestación
esencial del balance y la proporción
(especialmente en épocas antiguas y
hasta el medioevo). Una de las obras de arte
más admiradas por el mundo es la escultura
El David, de Miguel Ángel, que se considera
frecuentemente como una manifestación
de la perfección. Esta obra maestra
pone de manifiesto que muchas de las diferentes
proporciones, dentro de lo que se consideró
perfección en esa época, vienen
dadas por  . .
|
|
|