Adecuación de la ley de Gutenberg–Richter al contexto mexicano
Vol. 21, núm. 6 noviembre-diciembre 2020
Adecuación de la ley de Gutenberg–Richter al contexto mexicano
Ana Elena Posada Sánchez, Edgar Iram Villagrán Arroyo y Juan Pablo Hidalgo Toxqui CitaResumen
En nuestro país los sismos son uno de los fenómenos naturales que despiertan mayor atención, por lo que su estudio requiere contar con un adecuado monitoreo y sistemas de alerta, entre los que el teléfono inteligente parece una buena opción. En este trabajo se presenta un estudio, soportado en la base de datos del Servicio Sismológico Nacional y en la ley de distribución de magnitudes sísmicas propuesta por Gutenberg y Richter –único modelo aceptado a nivel mundial–, para explicar la probabilidad de ocurrencia de eventos sísmicos y sus magnitudes, de acuerdo con las regiones que presentan mayor cantidad de registros.
Palabras clave: sismo, magnitud, probabilidad de ocurrencia.
Adequacy of Gutenberg-Richter’s Law to the Mexican context
Abstract
In our country earthquakes are one of the natural phenomena that arises great interest, so their study requires adequate monitoring and alert systems, among which the smartphone seems as a good option. This work presents a study, supported by the National Seismological Service database and the seismic magnitudes distribution law proposed by Gutenberg and Richter –the only model accepted worldwide–, to explain the probability of occurrence of seismic events, as well as their magnitudes, according to the regions with the highest number of records.
Keywords: earthquake, magnitude, probability of occurrence.
Introducción
Los sismos son uno de los fenómenos que más afectan a la República mexicana, particularmente porque el país se ubica en una región en la que se perciben con gran intensidad, como ocurrió con los eventos del 8 y 19 de septiembre de 2017 (ssn, 2017a, 2017b) y, más recientemente, el 23 de junio de 2020 (ssn, 2020). Aunque mucho hemos avanzado en materia de prevención, lo cierto es que, hasta este momento, nadie puede decir cuándo ni a qué hora sucederá el próximo terremoto. Esta incertidumbre nos hace temer por el bienestar de nuestras familias y el propio, lo que nos lleva a buscar cualquier medio que nos permita estar un paso adelante de la contingencia.
En el presente trabajo encontrarás una estimación matemática de la probabilidad de ocurrencia de eventos de pequeña, mediana y gran magnitud, en función de los datos estadísticos recopilados hasta la fecha, que pretende responder a la pregunta: ¿cómo responde la sismicidad de México a la ley de Gutenberg-Richter?
Antecedentes
Ya desde el año 1944, los sismólogos Beno Gutenberg y Charles Francis Richter (g-r, Gutenberg y Richter, 1944) propusieron un modelo matemático que relaciona la magnitud de un evento sísmico con la ocurrencia de dicha magnitud en un intervalo de varios años –ver ecuación (1)–. A pesar de su simplicidad, el modelo ha demostrado ser muy acertado, independientemente de la región o del tiempo. Estrictamente hablando, los valores sí dependen de la región cuando ésta es relativamente pequeña, pero su variación no es muy significativa.
log10 N = a + b * M —————- (1)1
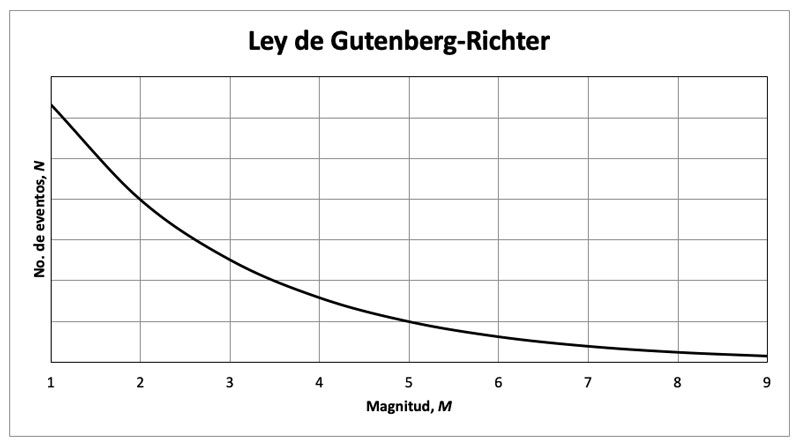
Figura 1. Representación gráfica del modelo Gutenberg-Richter. . Como se puede observar, existe una cantidad mucho mayor de eventos de magnitud 1 que de magnitud 2 y mayor cantidad de eventos de magnitud 7 que de magnitud 8, pero la proporción entre una diferencia y la otra se reduce considerablemente cuando avanzamos hacia magnitudes mayores en la gráfica.
En la expresión (1), n es el número de sismos que se espera se produzcan con magnitud m. a representa la actividad sísmica de la región en estudio y b la proporción logarítmica2 entre sismos grandes y sismos pequeños. La figura 1 presenta cualitativamente la curva que se genera al aplicar el modelo, en donde el eje vertical representa el número de eventos n y el eje horizontal corresponde a su magnitud. De acuerdo con cada región, los valores de a y b pueden variar y son, precisamente ellos, los que caracterizan el comportamiento de cada región.
La magnitud de un sismo es, en resumidas cuentas, una medida de la energía que se libera al romperse las placas tectónicas (Significados, 2019), cuando chocan o rozan (ver figura 2). La forma en que este valor se mide ha variado con el tiempo, actualmente se cuenta con un procedimiento estandarizado para su cálculo y es al que nos referimos en este artículo, si estás interesado en conocer las distintas formas de cuantificar la magnitud, lo puedes hacer aquí. (ssn, 2019a)
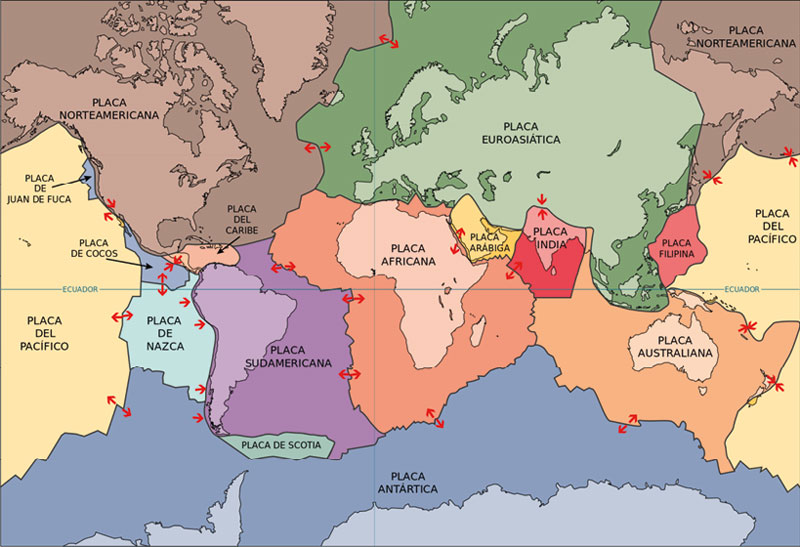
Figura 2. Placas tectónicas en el mundo (tomado de usgs, 2019). Recuperado de Wikimedia Commons.
El hecho de que el término izquierdo de la ecuación (1) sea logarítmico tiene una interpretación física importante y es que el cambio de un entero en magnitud implica una energía liberada 32 veces mayor. Aclaremos esto mediante la analogía de la tabla 1. Si equiparamos la cantidad de energía necesaria para generar un sismo de magnitud 1 con el precio en pesos mexicanos, ésta equivaldría al costo de un dulce o 1 peso. La cantidad de energía para un sismo de magnitud 2 sería equiparable al precio de 6 viajes en metro, o 32 pesos, etcétera. Siguiendo esta lógica, un evento de magnitud 7 correspondería al presupuesto anual para la infraestructura de Ciudad Juárez, Chihuahua, y este no es el valor máximo de la escala.
Analogía entre magnitud sísmica y unidades monetarias.
| Magnitud | Producto equivalente | Precio en pesos mexicanos |
|---|---|---|
| 1 | 1 dulce | 1 |
| 2 | 6 viajes en el metro | 32 |
| 3 | 2 pares de zapatos | 1,024 |
| 4 | Enganche para un auto económico | 32,768 |
| 5 | 1 departamento sencillo | 1,048,576 |
| 6 | Un fraccionamiento pequeño | 33,554,432 |
| 7 | Presupuesto anual estimado para infraestructura en Ciudad Juárez, Chih. (Olmos, 2019) | 1,073,741,824 |
| 8 | Presupuesto anual estimado para infraestructura en la CDMX (Cantera, 2019) | 34,359,738,368 |
| 9 | 7.2 veces el presupuesto original para la construcción del Tren Maya (Celis, 2019) | 1,090,000,000,000 |
Sismos en México
En México se cuenta con bases de datos de eventos medidos por el Servicio Sismológico Nacional (ssn, 2019). Seleccionamos los estados en los que se genera la mayor cantidad de sismos, más no los estados en los que son percibidos, incluso con gran intensidad. Por lo tanto, no se considera a la Ciudad de México, pues no es zona de generación de sismos de gran magnitud. Al revisar la información publicada, se pudo apreciar que los eventos con magnitud inferior a 3 son escasos en cuanto a número de registros se refiere, lo que indica que o no se registran todos o no se reportan, debido a que son prácticamente imperceptibles para nosotros.
Para este análisis, se tomaron en cuenta los eventos con magnitudes entre 3 y 8, ya que, de acuerdo con los registros del Servicio Sismológico Nacional, no se ha registrado algún evento de magnitud igual o mayor a 9 en el país.
Como lo indica Amador (2016), existe una relación lineal entre el logaritmo base diez del número de eventos y su magnitud; por lo tanto, es posible emplear el método de regresión por mínimos cuadrados3 para calcular los parámetros a y b de cada región.
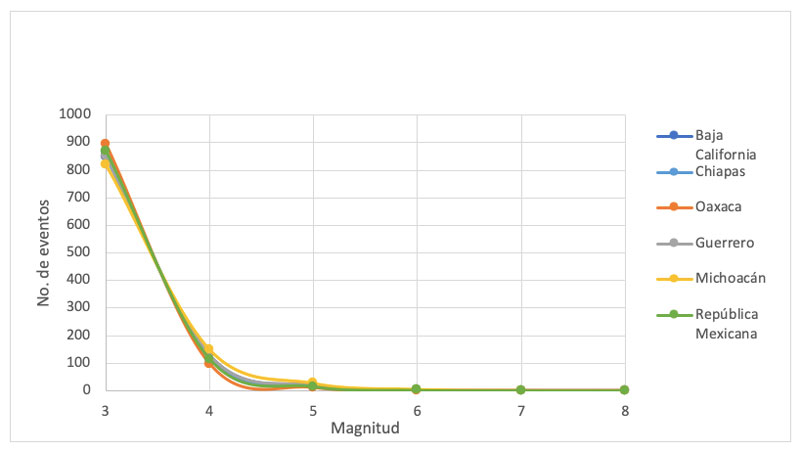
Figura 3. Distribución de magnitudes por cada 1000 eventos. Se observa que la cantidad de eventos registrados de magnitud 3 es considerablemente superior a los de magnitud 4, la cantidad de eventos de magnitud 4 es mayor que los de magnitud 5, pero en menor proporción, y así sucesivamente. La variación no es exactamente igual para todos los estados, pero los comportamientos de las diferentes curvas son muy similares.
Una vez realizada la correlación matemática correspondiente a cada estado (cálculo de los valores de a y b), se encontró que la forma de la curva que corresponde a la ley de Gutenberg-Richter para los estados analizados es la que se presenta en la figura 3.
Como se puede observar, la ley de Gutenberg-Richter representa con gran precisión la relación entre magnitud y número de eventos para los estados seleccionados. Los parámetros a y b para cada estado oscilan entre 5.95 y 7.75 para el valor de a, mientras que van de -0.743 y -0.971 para el valor de b.
La figura 3 muestra la distribución de los eventos según estos parámetros, mismos que fueron ajustados para 1000 eventos y no de forma temporal como sugieren Gutenberg y Richter, sin embargo, y como se aprecia, este número es suficiente para observar la tendencia.
Aplicando la ley
Plantearemos una segunda pregunta, ¿cuántos sismos de magnitud menor a 3 y cuántos de magnitud 9 o superior se podrían esperar dadas las mediciones realizadas? Para resolver la pregunta se emplearon los valores de a y b del paso anterior para conocer la distribución de probabilidades, no solamente de lo registrado, sino también de lo que no, es decir, sismos “pequeños”, menores a 3, y “muy grandes”, iguales o mayores a 9. Al mismo tiempo, se ajustaron los valores de tal manera que apareciera por lo menos un evento de magnitud 9. A este procedimiento se le conoce como extrapolación. La tabla 2 muestra esta variación.
Proporción entre eventos de diferentes magnitudes respecto de uno con magnitud 9 o superior.
Estados |
|||||
|---|---|---|---|---|---|
| Magnitud | Baja California | Chiapas | Guerrero | Michoacán | Oaxaca |
| 1 | 3,527,246 | 9,712,500 | 4,036,145 | 881,113 | 58,976,255 |
| 2 | 535,804 | 1,299,914 | 602,866 | 159,185 | 6,300,029 |
| 3 | 81,391 | 173,980 | 90,048 | 28,759 | 672,989 |
| 4 | 12,364 | 23,285 | 13,450 | 5,196 | 71,891 |
| 5 | 1,878 | 3,116 | 2,009 | 939 | 7,680 |
| 6 | 285 | 417 | 300 | 170 | 820 |
| 7 | 43 | 56 | 45 | 31 | 88 |
| 8 | 7 | 7 | 7 | 6 | 9 |
| 9 | 1 | 1 | 1 | 1 | 1 |
| Porcentaje de eventos de la base analizada | 3% | 18% | 16% | 4% | 38% |
En la tabla 2 se presentan los porcentajes por estado con respecto al total de eventos de la base de datos, que es de 166,488 temblores, registrados a partir del año 1900 hasta mayo de 2019.
La última fila suma 79%, ya que no incluye los eventos registrados en los estados no considerados, ni aquellos cuya magnitud fue no calculable, por presentar una sismicidad muy pequeña.
La tabla 2 puede crear alguna confusión al hacer una comparación simple de los valores. En primer lugar, no significa que, por ejemplo, en Oaxaca por cada 59 millones de temblores de magnitud 1, sucedan 820 de magnitud 6 o 9 de magnitud 8. Tampoco significa que hay que contar 88 sismos de magnitud 7 para que suceda uno de magnitud 9. Lo que nos dice la ley de Gutenberg-Richter es que es más probable que se generen sismos de baja magnitud a lo largo del tiempo (en realidad muchos años), a que se presenten eventos muy destructivos para nosotros; sin embargo, el que sean poco probables no los convierte en imposibles.
Tampoco se debe pensar que Guerrero requiere menos sismos de magnitud 7 que Chiapas para tener una probabilidad de un evento magnitud 9. Lo que debe interpretarse es que en Guerrero se registran menos movimientos telúricos que en Chiapas para el mismo intervalo de tiempo, lo que significa que en Guerrero se requieren más años para tener la misma probabilidad.
Para aclarar lo anterior, supongamos que se lanza una moneda y se cuenta el número de águilas y de soles. La probabilidad indica que, con el suficiente número de lanzamientos, el porcentaje de unas y otros será del 50%. Esto no significa que en el proceso no puedan salir, por ejemplo, cuatro águilas seguidas. La naturaleza de los sismos es similar, sólo que su moneda tiene 9 caras (y sus fracciones), y está cargada hacia los valores menores.
Otro punto importante es que la división geopolítica de México poco tiene que ver con los mecanismos de generación de terremotos. Una división geográfica más adecuada para comprender la sismicidad consistiría en generar una gran región que abarcara todos aquellos sitios en los que la sismicidad es alta, por ejemplo, Chiapas-Michoacán. Con esto se tendría que la variación de los valores a y b, mencionados al inicio, tienen que ver más con una división arbitraria del territorio que con la sismicidad.
Consideramos ahora los últimos 10 años de reportes del ssn y los presentamos en la tabla 3 (ssn, 2019).
Eventos reportados cada año por el ssn en la última década.
| Año | Número de sismos reportados |
|---|---|
| 2009 | 2301 |
| 2010 | 3462 |
| 2011 | 4272 |
| 2012 | 5244 |
| 2013 | 5361 |
| 2014 | 7608 |
| 2015 | 10946 |
| 2016 | 15547 |
| 2017 | 26363 |
| 2018 | 30193 |
Nuevamente alertamos sobre la interpretación simple de los números. La tabla 3 no indica que el número de sismos sea cada vez mayor, la verdadera razón de este incremento obedece a que hay más y mejores equipos cada año (y con ello más trabajo), lo que habla muy bien del ssn. Sin embargo, el hecho de que empecemos a medir algún fenómeno no significa que acaba de iniciar. Tratar de acoplarnos al conteo es muy complicado porque empezó hace millones de años, pero se espera que, con el tiempo, el número de sismos registrados anualmente se llegue a estabilizar alrededor de una cifra, por lo que los valores de a y b tenderán a tener menor variación.
El Sistema de Alerta Sísmica Mexicano (sasmex) y algunas aplicaciones para dispositivos móviles son hasta ahora la mejor opción que se tiene para mitigar los efectos negativos que puede generar un evento sísmico de gran magnitud sobre la población. Es conveniente conocer las restricciones con las que cuenta cada una de estas aplicaciones, por ejemplo, los segundos previos al arribo de las ondas generadas por un sismo que acaba de ocurrir en un sitio distante.
Conclusión
La apuesta “a que tiembla mañana” es casi segura, siempre y cuando no se establezca ni el epicentro ni la magnitud, puesto que, como podemos ver en la tabla 3, en 2018 se registraron casi 100 sismos por día, en promedio. El conocimiento de la probabilidad de ocurrencia sólo nos permite describir la forma en que el fenómeno se presenta estadísticamente para la república Mexicana y para algunos estados; sin embargo, sigue sin poder considerarse como una herramienta de predicción. Por lo anterior, la mejor recomendación que puede hacerse con respecto a la probable ocurrencia de sismos de gran magnitud es estar alerta y contar con planes de contingencia que incluyan el qué hacer antes, durante y después de un sismo de mediana o gran magnitud (unam, 2020).
Referencias
- Amador C., Z. (2016). Terremotos como sistemas complejos: estudio de la ley de Gutenberg-Richter [presentación] https://ergodic.ugr.es/jmarro/fisico/pages/16Amador-Terremotos.pdf.
- Cantera, S. (2019, 28 de enero). Industria de la Construcción estima inversión por 30 mil mdp para la Ciudad de México. El Universal. https://www.eluniversal.com.mx/cartera/economia/industria-de-la-construccion-estima-inversion-por-30-mil-mdp-para-la-ciudad-de.
- Celis, F. (2019, 26 de junio). Gobierno no aumentará presupuesto de 150,000 mdp para el Tren Maya:Fonatur. Forbes, México. https://www.forbes.com.mx/gobierno-no-aumentara-presupuesto-de-150000-mdp-para-el-tren-maya-fonatur/.
- cenapred. (2020). Sistemas de Alerta Temprana [infografía]. Centro Nacional de Prevención de Desastres, Ciudad de México. www.cenapred.gob.mx/es/Publicaciones/archivos/298-INFOGRAFASISTEMASDEALERTATEMPRANA.pdf.
- Gutenberg, B. y C. F. Richter. (1944). Frequency of Earthquakes in California. Bulletin of the Seismological Society of America, 185-188, California Institute of Technology.
- Olmos, J. (2019, 6 de marzo). Plantean invertir mil mdp en obras para Juárez. El Diario de Juárez. https://diario.mx/juarez/plantean-invertir-mil-mdp-en-obras-para-juarez-20190306-1486499/.
- Servicio Sismológico Nacional. (2017). Sismo de tehuantepec (2017-09-07 23:49 mw 8.2) [elaborado el 7 de septiembre de 2017 y actualizado el 28 de noviembre de 2017]. http://www.ssn.unam.mx/sismicidad/reportes-especiales/.
- Servicio Sismológico Nacional. (2017). Sismo del día 19 de Septiembre de 2017, Puebla-Morelos (M 7.1) [elaborado el 25 de septiembre de 2017]. http://www.ssn.unam.mx/sismicidad/reportes-especiales/.
- Servicio Sismológico Nacional. (2019). Magnitud de un sismo. http://www.ssn.unam.mx/jsp/reportesEspeciales/Magnitud-de-un-sismo.pdf.
- Servicio Sismológico Nacional. (2019). Catálogo de sismos. http://www2.ssn.unam.mx:8080/catalogo/.
- Servicio Sismológico Nacional. (2020). Sismo del 23 de junio de 2020, Costa de Oaxaca (M 7.4) [elaborado el 23 de junio de 2020 y actualizado el 24 de junio de 2020]. http://www.ssn.unam.mx/sismicidad/reportes-especiales/.
- Significados. (2019). ¿Qué son las placas tectónicas? https://www.significados.com/placas-tectonicas/.
- unam. (2020). ¿Qué hacer en caso de sismo? https://www.unam.mx/medidas-de-emergencia/sismos.
- usgs. (2014). Las 15 placas tectónicas mayores [versión en español Daroca90 cc by-sa 3.0]. http://pubs.usgs.gov/publications/text/slabs.html.
Recepción: 01/07/2019. Aprobación: 30/06/2020.


