Cuasicristales: de universos paralelos a sombras multidimensionales

Resumen

Este texto se encuentra en el límite de la física de los materiales, la geometría y la topología. Comenzamos exponiendo el concepto topológico de espacio localmente isomorfo, a través de un experimento mental, en el que nos transportamos a un universo paralelo. Después, para poder hablar de cuasicristales, revisamos cuáles son los diferentes estados de la materia y sus propiedades principales. En seguida, presentamos la historia sobre el descubrimiento de los cuasicristales para seguir la discusión sobre las matemáticas que los describen, en especial la interpretación de los cuasicristales como proyecciones geométricas de cristales periódicos de dimensiones mayores (es decir, espacios donde las coordenadas requieren más de tres valores). Relacionamos la interpretación en altas dimensiones con las perturbaciones termodinámicas que describen la conductividad térmica y con ello regresamos al concepto de espacio localmente isomorfo y a ese un universo paralelo inicial.
Palabras clave: cuasicristales, isomorfismo, estados de la materia, termodinámica, conductividad térmica.

Quasicrystals: from parallel universes to multidimensional shadows

Abstract

This text lies at the boundary of materials physics, geometry and topology. We begin by exposing the topological concept of locally isomorphic space, through a thought experiment, in which we are transported to a parallel universe. Next, to talk about quasicrystals, we review the different states of matter and their main properties. Afterwards, we present the story of the discovery of quasicrystals to continue the discussion on the mathematics that describes them, especially the interpretation of quasicrystals as geometric projections of periodic crystals of higher dimensions (that is, spaces where the coordinates require more than three values). We relate the interpretation in high dimensions with the thermodynamic perturbations that describe thermal conductivity and with this we return to the concept of locally isomorphic space and that an initial parallel universe.
Keywords: quasicrystals, isomorphism, state of matter, thermodynamics, thermal conductivity.

---

Introducción

Imagina que una mañana despiertas con la sensación de que no estás en tu casa, que te han teletransportado a un universo casi idéntico, pero que no es el tuyo. Con el objetivo de descubrir si se trata de tu universo o uno paralelo, sales en búsqueda de cualquier posible detalle que sea diferente. Después de recorrer algunos kilómetros en las vecindades de tu casa, concluyes que era sólo una sensación, que en realidad te encuentras en tu universo, o al menos, en una copia idéntica que para todo fin práctico es exactamente lo mismo.

Pero ¿cómo podrías estar completamente seguro de que no existe ninguna diferencia con el universo que tú conoces en algún lugar que no has revisado? ¿Qué tal que el universo en el que estás es idéntico sólo a unos pocos kilómetros a la redonda y después comienzan a notarse los cambios? Esa noche se te ocurre una buena prueba: mirar al cielo para asegurarte de que las estrellas están donde deberían estar. Al observar el cielo descubres impactado que, aunque se parece muchísimo al que conoces, la distribución de las estrellas no es la habitual y el cinturón de Orión tiene cuatro estrellas en vez de tres. Por lo tanto, te encuentras en un universo paralelo, en uno localmente isomorfo.

Pero ¿qué significa que algo sea localmente isomorfo? La palabra isomorfo proviene del griego iso (igual) y morphe (forma), de modo que, si un espacio es localmente isomorfo a otro, lo que esto nos indica es que ambos tienen, localmente, la misma forma o bien, que son localmente iguales.

Esta definición no precisa qué tan local es lo local, es decir, hasta qué distancia o dentro de qué región deben ser dos sistemas idénticos para ser considerados localmente isomorfos. Para evitar complicaciones podemos decir que esas regiones son cualquier región, sin importar qué tan grande sea, siempre y cuando sea finita. Vamos a decir que dos universos, A y B, son localmente isomorfos si para cada región finita que elijamos en el universo A hay una región idéntica en el universo B y viceversa. Seguramente estuviste intentado imaginar cómo sería eso y concluiste que esta definición implica que ambos universos sean idénticos. Para universos finitos esto es verdadero. Dos universos finitos son localmente isomorfos sólo si son idénticos en su totalidad, pues podríamos elegir, como nuestra región en A, al mismo universo A y en B elegir el mismo B. En el caso de universos infinitos, esto deja de ser verdadero porque ya no podemos elegir a todo el universo como la región. Puede haber dos universos que sean diferentes, pero localmente isomorfos.

Los objetos localmente isomorfos están íntimamente relacionados con cómo se almacena el calor en algunos cristales cuyas dimensiones, de alguna forma, son mayores a tres. Entre estos cristales de dimensiones altas, los más comunes que se producen son de seis dimensiones. Hablaremos con más detalles de ellos un poco más adelante, pero antes necesitamos adentrarnos al mundo de la termodinámica para poder entender cómo se produjeron los primeros de estos cristales multidimensionales.

Fases de la materia

El calor y la temperatura son dos conceptos que tratamos casi como sinónimos: si tenemos calor dentro de una habitación, prendemos el aire acondicionado para que baje la temperatura, o bien, si tenemos frío, subimos la temperatura para sentir más calor. Sin embargo, una reducción del calor no siempre implica una reducción en la temperatura. Por ejemplo, si ponemos agua en el congelador y medimos cada 5 minutos la temperatura, obtendremos una gráfica como la de la figura 1. Primero la temperatura baja hasta llegar a cero grados centígrados. Después la temperatura se estanca durante horas y finalmente vuelve a bajar. Cuando el agua está a cero grados, extraer calor no reduce la temperatura, sino que produce enlaces entre las moléculas, lo que forma hielo. Este proceso se conoce como una transición de fase de primer tipo.

Las diferentes fases de la materia están separadas por una transición de fase. Si al agregar o quitar calor observamos un cambio abrupto en alguna propiedad física (cambios en el calor, la viscosidad, propiedades eléctricas, entre otros), entonces sabemos que pasamos de una fase a otra. Para decir que hay una nueva fase de la materia se agrega o extrae calor del material de interés y se observa si la temperatura en algún momento se estanca o si de forma abrupta cambia alguna propiedad del material.

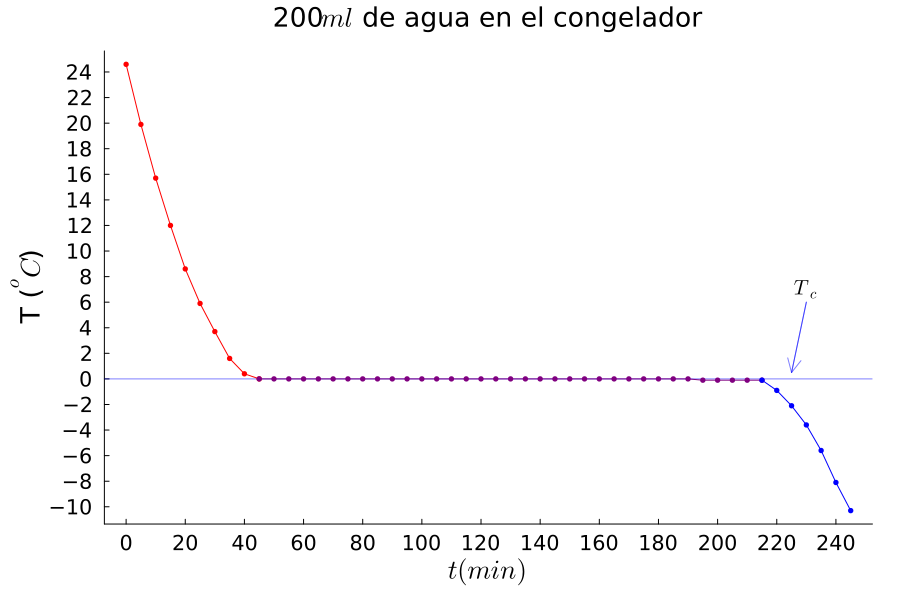
Figura 1. Curva de enfriamiento del agua líquida y el hielo.
Crédito: elaboración propia.

Esta estrategia nos ha llevado a encontrar una gran variedad de fases de la materia. No sólo hay sólidos, líquidos y gases, sino que entre los gases está el plasma y gases comunes, entre los líquidos hay líquidos comunes, superfluidos, cristales líquidos, etcétera, y entre los sólidos podemos encontrar diferentes estructuras cristalinas de la misma molécula, llamadas alotropías. Por ejemplo, para el hielo se conocen 19 alotropías (Hansen, 2021), es decir, existen por lo menos 19 tipos diferentes de hielo, mientras que para el oxígeno sólido se conocen seis tipos de fases (Freiman y Jodl, 2004), cada una de un color diferente: azul, rosa, naranja, rojo, negro y plateado.

Cristales

En general, como lo sugieren los ejemplos anteriores, el estado sólido cuenta con una gran variedad de fases. Sin embargo, no todas son estables, algunas son metaestables (es decir que, ante pequeños cambios en su entorno, pueden cambiar algunas de sus propiedades), por lo que si el enfriamiento del material es lento sólo pasará por las fases estables.

En los experimentos y cálculos que se han hecho, las fases estables en el estado sólido son siempre un cristal; es decir, un arreglo ordenado de moléculas. Aquí debemos aclarar qué significa ordenado. Hasta 1984, entre los científicos que estudiaban el estado sólido, ordenado significaba periódico. Periódico en este contexto significa que se repite cada cierta longitud en alguna dirección particular. Por ejemplo, una cuadrícula es un arreglo periódico porque cada vez que nos recorremos a la izquierda, derecha, arriba o abajo una longitud igual al lado de los cuadrados vemos exactamente la misma figura. Pasa lo mismo con un panal de abejas, donde esta vez los compartimentos son en forma de hexágono (ver figura 2). Cuando algo es periódico, como el panal de abejas o una cuadrícula, decimos que tiene simetría traslacional.

Figura 2. Simetría hexagonal presente en un panal de abejas.
Crédito: elaboración propia.

Los cristalógrafos habían notado que imponer una simetría traslacional en dos dimensiones imponía también que hubiera una simetría rotacional, es decir, si giramos un determinado ángulo nuestro sistema, este se verá exactamente igual. Por ejemplo, la cuadrícula tiene una simetría rotacional, porque al girarla 90° queda exactamente igual. En el caso de los hexágonos, el giro necesario para que ocurra esta situación es de 60°. En general, un polígono regular de N lados tendrá una simetría rotacional con un giro de 360°/N.

Para el caso de los cristales con simetría traslacional, las únicas posibilidades para su simetría rotacional son giros de 360°/N, con N = 2, 3, 4, o 6. En la figura 3 se muestran todas las simetrías rotacionales posibles en 2D. Notemos que, en particular, no aparece el caso N= 5.

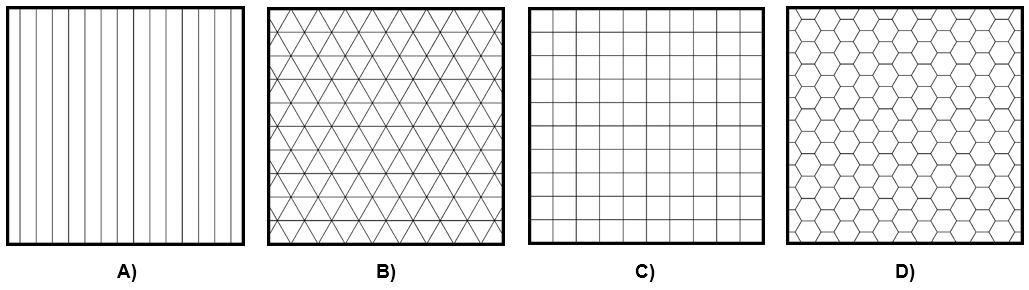
Figura 3. Simetrías rotacionales en 2D. A) N = 2. B) N = 3. C) N = 4. D) N = 6. Crédito: elaboración propia.

Si uno se va a tres dimensiones, con un poco más de esfuerzo, se concluye que hay 6 tipos diferentes de simetría rotacional. Si además de las simetrías rotacionales se consideran las reflexiones (es decir las estructuras que se obtienen de ponerlas frente a un espejo), para el caso 2D se descubre que hay 17 tipos diferentes de estructuras, mientras que para el caso 3D se obtiene un total de 230 (Luger, 2014). Son muchas posibilidades, pero finitas. Podríamos esperar, entonces, que para cada molécula todas las fases sólidas sean alguna de estas 230 estructuras.

Con el descubrimiento de los rayos X, los cristalógrafos tuvieron una herramienta muy poderosa para desenmascarar la estructura atómica de los diferentes sólidos. Muchos de ellos coincidían con las 230 estructuras predichas, pero no todos, ni siquiera la mayoría. Muchos de los sólidos parecían no ser cristales, sino tener sus átomos de forma desordenada, algo muy parecido a la estructura de los átomos en un líquido. A estos sólidos sin forma les llamaron amorfos. Los vidrios de una ventana son un ejemplo de estos sólidos amorfos, junto con plásticos y maderas.

Para lograr que un sólido sea amorfo, la regla general es comenzar con el material en estado líquido y enfriarlo muy rápidamente. Qué significa muy rápido depende del material. En el caso del SiO₂ (óxido de silicio) es bajar 100°C en menos de 2 semanas, mientras que en el caso del agua significa bajar los mismos 100°C en menos de 1 microsegundo. Por eso tenemos ventanas de SiO₂, pero no vemos hielo en forma amorfa, aunque sí es común en el espacio (O’Callaghan, 2023) debido a que allí la temperatura suele ser suficientemente baja para impedir la cristalización.

Unos párrafos arriba mencionamos que orden significaba periodicidad. Pero, en noviembre de 1984, cambió la visión de los cristalógrafos. Dan Shechtman, un físico israelí, publicó haber encontrado un cristal al que llamó cuasicristal, que tenía la misma simetría de un pentágono, es decir, tenía una simetría rotacional prohibida por la teoría cristalográfica de la época (Shechtman et al, 1984). Shechtman estaba intentando obtener un vidrio metálico de una aleación de aluminio y manganeso al bajar rápidamente la temperatura de la aleación. En su lugar obtuvo un cristal con una simetría rotacional prohibida N = 5. En 2011, Shechtman recibió el premio Nobel de química por su descubrimiento y por las implicaciones que tuvo en la teoría cristalográfica, pues esto representó un cambio de paradigma sobre los materiales que pueden existir, lo que amplió nuestro concepto de orden más allá de los sistemas periódicos.

Breve historia de los cuasicristales

La historia de los cuasicristales no comienza con Shechtman, sino en los años sesenta, con el lógico chino Hao Wang, quien trataba de hacer un programa de computadora que se dedicara a hacer demostraciones matemáticas (Wang, 1965). En su trabajo mostró que este programa podía existir sólo si dado un conjunto finito de teselas,1 siempre se podía teselar el plano de forma periódica. Pocos años después, su estudiante, Robert Berger, mostró un conjunto de 20,426 teselas diferentes que sólo podían teselar el plano de forma no periódica (Berger, 1966).

Durante la siguiente década, varios matemáticos fueron reduciendo el número de teselas necesarias hasta llegar a 2 teselas, conjunto obtenido por el físico y matemático británico Sir Roger Penrose (Gardner, 1977). Una curiosidad del trabajo de Penrose es que no se publicó en una revista de investigación, sino en Scientific American, una revista de divulgación, en la sección Matemática recreativa, área encargada de proponer y resolver problemas matemáticos desde un enfoque lúdico. La belleza de la solución de Penrose recae, entre otras cosas, en que posee una notable simetría pentagonal (ver figura 4). En su artículo original, Penrose se limitó a mostrar que la configuración obtenida es “aperiódica” aunque en realidad lo que Penrose generó fue una estructura que hoy conocemos como cuasiperiódica.2

Figura 4. Ejemplo de un teselado de Penrose alrededor de su centro de simetría. Crédito: elaboración propia.

Cuasicristales y cristales en altas dimensiones

Cuatro años después del trabajo de Penrose, el matemático holandés Nicolaas de Bruijn mostró un método para generar estructuras cuasiperiódicas proyectando en el plano (o espacio) una estructura periódica en altas dimensiones (de Bruijn, 1981). En el trabajo de de Bruijn, se obtenía el teselado de Penrose como una proyección de una hipercubícula3 5-dimensional, así como un arreglo similar en tres dimensiones llamado icosaédrico al proyectar una hipercubícula 6-dimensional en un espacio 3-dimensional. A lo largo de los siguientes años se fueron encontrando múltiples cuasicristales, cada uno asociado a un cristal de dimensión mayor a tres.

El poder describir la estructura de un cuasicristal como la proyección de un objeto en una dimensión mayor no significa que el objeto realmente esté en una dimensión mayor, se trata sólo de un truco matemático. Por ejemplo, podemos ver un hexágono como la proyección de un cubo (3-dimensional) en el plano (2-dimensional), pero eso no significa que los hexágonos sean siempre la sombra de un cubo, pueden producirse por muchas otras razones.

Entre vidrios y cristales

El mismo año que de Bruijn publicó su trabajo, Paul Steinhardt y su equipo realizaron una serie de experimentos numéricos para tratar de simular la formación de vidrios metálicos al reducir rápidamente la temperatura del metal (Steinhardt, et al, 1981). En sus trabajos, encontraron la formación de estructuras desordenadas con una aparente simetría icosaédrica en sus enlaces. A partir de estos resultados, desarrollaron durante los siguientes tres años una teoría que permitió la formación de sólidos ordenados con dicha simetría (Steinhardt, et al, 1983; Chaudhari, et al, 1983; Levine y Steinhardt, 1984). Los sólidos generados por esta teoría son los mismos que Schechtman encontró en sus experimentos. Estos fueron los primeros trabajos donde se estudiaron los cuasicristales desde un punto de vista físico y no matemático. Así, el mérito de Steinhardt y su equipo fue reconocer que las estructuras que encontraron mediante un proceso físico, y que más tarde se conocerían como cuasicristales, eran un equivalente a los teselados de Penrose, pero en 3 dimensiones.

Capacidad calorífica de los cristales y cuasicristales

Una vez relacionado el concepto geométrico de teselado cuasiperiódico con un material físico, lo natural es preguntarse por sus propiedades físicas. Una de las más importantes en cualquier material es su capacidad calorífica C_v. Esta mide cuánto calor es necesario agregar para aumentar un grado centígrado la temperatura.

Los gases y líquidos mantienen aproximadamente la misma capacidad calorífica de manera independiente a la temperatura, es decir, cuesta lo mismo elevar la temperatura del vapor de agua de 101 °C a 102 °C, que de 200 °C a 201 °C. Los cristales, en cambio, tienen una capacidad calorífica que depende de la temperatura de una forma más o menos complicada. Para temperaturas altas se parece a la de un gas, pero a temperaturas bajas, la capacidad calorífica de los cristales (en tres dimensiones) tiene una función cúbica de la temperatura, es decir: C_v (T) ~ T3.

La explicación de ese fenómeno se la debemos a Peter Debye, un físico holandés-estadounidense. Debye, además de haber sido espía durante la segunda guerra mundial, hizo una sofisticada teoría que utiliza tanto herramientas de mecánica cuántica como de termodinámica, para explicar el comportamiento de la capacidad calorífica a temperaturas bajas (Pathria, 2011). En su teoría, Debye pensó a los cristales como una especie de sistema de masas y resortes, donde las masas estaban en las posiciones de las moléculas y los resortes representaban los enlaces entre éstas. Al mover una de las masas, debido a los resortes, se propaga una onda que viaja dentro del cristal. Esa onda, que se puede propagar en las tres dimensiones del cristal, tiene una frecuencia que depende de la separación entre las moléculas. Con ello y usando el hecho de que las ondas son también partículas según la mecánica cuántica, logró obtener una capacidad calorífica que era muy similar a los resultados experimentales. Las partículas resultado de las vibraciones de las moléculas del cristal se llaman fonones y se pueden observar experimentalmente utilizando una técnica conocida como espectroscopía Ramman.

En el caso de los cuasicristales, la capacidad calorífica obtenida de manera experimental no coincide con la capacidad calorífica que se obtiene computacionalmente a partir de la formación de fonones. La explicación está en las dimensiones extra. Si uno aplica el modelo de Debye al cristal en altas dimensiones y después lo proyecta en el espacio real, aparece un nuevo tipo de ondas que se mueven en las dimensiones extra. Las partículas asociadas a estas ondas en las dimensiones extra se conocen como fasones (de Boissieu, 2019). Los fasones se ven en el cuasicristal como un reordenamiento de las moléculas, cambiando de una estructura cuasiperiódica a otra muy similar. Este reordenamiento se genera en todo el cuasicristal de forma casi instantánea. Lo interesante es que tomando en cuenta estas partículas en las dimensiones extra, la capacidad calorífica del cuasicristal medida experimentalmente y la calculada numéricamente coinciden.

Esto, nuevamente, no significa que el cuasicristal sea realmente un cristal en más de tres dimensiones, pero se comporta como si lo fuera, tanto en su estructura, como en la dinámica de sus moléculas. Podemos, entonces, fantasear con que realmente el cuasicristal de Shechtman vive en un espacio 6-dimensional y lo que vemos es sólo la “sombra” de este cristal 6-dimensional.

Localmente isomorfo

Ya estamos preparados para volver a nuestra discusión de los universos localmente isomorfos, sólo que, en lugar de universos hablaremos de cuasicristales.

Poner las moléculas en una posición determinada cuesta energía. Si vamos colocando una por una, la primera no nos costará energía, pero una vez que está colocada la primera molécula, habrá fuerzas electrostáticas que harán que cueste una energía diferente poner la nueva molécula en una posición u otra. Una vez colocada la segunda molécula, la posición de la tercera también tendrá un costo diferente dependiendo de la posición que elijamos y así sucesivamente para todas las moléculas. Así, sabemos que la energía que se requiere para construir un arreglo de moléculas en estado sólido depende de la distancia que haya entre cada par de moléculas. Si tenemos N moléculas, tendremos (N² – N) / 2 distancias entre las moléculas. Entonces, para todo conjunto de N moléculas y (N² – N) / 2 distancias se tiene definida una energía, pero para cada energía no necesariamente se tiene un solo conjunto de N átomos y (N² – N) / 2 distancias, podrían ser varias posibilidades. En particular, si dos estructuras son localmente isomorfas el conjunto de moléculas y distancias es igual en ambas estructuras y, por lo tanto, se requiere la misma energía para construirlas. Dos estructuras localmente isomorfas tienen el mismo costo energético.

Al conjunto de todas las estructuras que son isomorfas localmente entre sí se le llama clase de isomorfismo local. Se puede mostrar que todos los cuasicristales pertenecen a alguna clase de isomorfismo con una infinidad de elementos (Levine, 1986). Es decir, para cada cuasicristal ideal existe una infinidad de cuasicristales que son localmente isomorfos. También se puede mostrar que, si una clase de isomorfismo tiene más de un elemento, entonces, tiene una infinidad y todos los elementos son cuasiperiódicos.

Esto tiene como consecuencia que se puede pasar de un cuasicristal a otro sin que cueste nada de energía, si pertenecen a la misma clase de isomorfismo local. Como no cuesta energía, el efecto final es que en un cuasicristal real los átomos no están fijos realmente, sino que se reordenan todo el tiempo, recorriendo todos los elementos de la misma clase de isomorfismo. Esos reordenamientos son justamente los fasones de los que hablamos antes.

Regresemos a nuestra historia del inicio, donde despertamos en un universo paralelo localmente isomorfo. Por lo que aprendimos de los cuasicristales, si dicho universo existiera, existirían una infinidad de ellos y no sólo podría pasar que despertaras en uno de estos, sino que de hecho estarías recorriéndolos todos, cambiando en cada momento a un nuevo universo, oscilando entre todos ellos, algo que también podríamos ver como que en realidad nuestro universo es de más dimensiones y nos movemos no sólo en aquellas que vemos, sino también en las dimensiones extra.

Agradecimientos

Los autores agradecemos el apoyo económico por parte del proyecto PAPIIT IN113923.

Referencias

• Berger, R. (1966). The undecidability of the domino problem. American Mathematical Society. https://tinyurl.com/ymkjxr25.
• Chaudhari, P., Spaepen, F., y Steinhardt, P.J. (1983). Defects and atomic transport in metallic glasses. En H. Beck y HJ. Güntherodt (Eds.), Glassy Metal ii (pp. 127-168). Springer. https://link.springer.com/content/pdf/10.1007/3540127879_27.pdf .
• de Boissieu, M. (2019). Ted Janssen and aperiodic crystals. Acta Crystallographica Section A, 75(2), 273-280. https://doi.org/10.1107/S2053273318016765.
• de Bruijn, N.G. (1981). Algebraic theory of Penrose’s non-periodic tilings of the plane, II. Indagationes Mathematicae (Proceedings), 84(1), 53-66. https://pure.tue.nl/ws/portalfiles/portal/4344195/597566.pdf.
• Freiman, Y. A., y Jodl, H. J. (2004). Solid oxygen. Physics Reports, 401(1-4), 1-228. https://doi.org/10.1016/j.physrep.2004.06.002.
• Luger, P. (2014). Modern X-Ray Analysis on Single Crystals: A Practical Guide. (2.^a ed.). De Gruyter. https://doi.org/10.1515/9783110308280.
• Gardner, M. (1977). Mathematical games: Extraordinary nonperiodic tiling that enriches the theory of tiles. Scientific American, 236, 110-121. https://doi.org/10.1038/scientificamerican0177-110.
• Hansen, T. C. (2021). The everlasting hunt for new ice phases. Nature Communications, 12, 3161. https://doi.org/10.1038/s41467-021-23403-6.
• Levine, D., y Steinhardt, P. J. (1984). Quasicrystals: A New Class of Ordered Structures. Physical Review Letters, 53(26), 2477-2480. https://doi.org/10.1103/PhysRevLett.53.2477.
• Levine, D. (1986). Local isomorphism, Landau theory, and matching rules in quasicrystals. Le Journal de Physique Colloques, 47(C3), 125-134. https://doi.org/10.1051/jphyscol:1986312.
• O’Callaghan, J. (2023). Scientists made a new kind of ice that might exist on distant moons. Nature, 614, 396-397. https://doi.org/10.1038/d41586-023-00293-w.
• Pathria, R. K., y Beale, P. D. (2011) Statistical Mechanics. (3^a ed.). Elsevier.
• Shechtman, D., Blech, I., Gratias, D., y Cahn, J. W. (1984). Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Physical Review Letters, 53(20), 1951-1953. https://doi.org/10.1103/PhysRevLett.53.1951.
• Steinhardt, P. J., Nelson, D. R., y Ronchetti, M. (1981). Icosahedral Bond Orientational Order in Supercooled Liquids. Physical Review Letters, 47(18), 1297-1300. https://doi.org/10.1103/PhysRevLett.47.1297.
• Steinhardt, P. J., Nelson, D. R., y Ronchetti, M. (1983). Bond-orientational order in liquids and glasses. Physical Review B, 28(2), 784-805. https://doi.org/10.1103/PhysRevB.28.784.
• Wang, H. (1965). Games, Logic and Computers. Scientific American, 213(5), 98-107. http://www.jstor.org/stable/24931186.

Recepción: 26/08/2023. Aprobación: 12/03/2024.