Resumen

No todos los átomos de un mismo elemento son iguales, algunos son más pesados que otros. Esto se debe a que varían en el número de neutrones que los componen. Así, a los átomos del mismo elemento con diferente masa molecular, debido a variaciones en el número de neutrones, se les conoce como isótopos. Estos parientes “gordos” tienen propiedades muy particulares, que los han vuelto una herramienta de estudio en un sinnúmero de ramas de la ciencia: desde determinar el origen de nuestra luna, el mapeo de la historia climática de la Tierra o la dieta humana, hasta el estudio de las ciencias forenses. En este artículo mostramos cómo el estudio de los isótopos da resultados novedosos e interesantes para la solución de toda clase de preguntas científicas.

Isotopes: The Fat Twins of Chemical Elements

Abstract

Not all atoms of an element are equal, some are heavier than others. This is because they vary in the number of neutrons they contain. Thus, atoms of the same element with different molecular masses, due to variations in the number of neutrons they contain, are known as isotopes. This “fat” relatives have unique physical properties, making them an essential tool in multiple scientific areas: from determining the origins of the moon, mapping the climatic history of Earth or the human diet, to the study of forensic sciences. In this article we show how studying isotopes yields interesting and novel results to solve all sorts of different scientific questions.

Introducción

¿Alguna vez has encontrado a alguien idéntico a ti, pero en una ciudad distinta, con distinto peinado, más gordo o más flaco? Y, aun así, te da la sensación de parecerse tanto a ti, que te hace creer que es tu gemelo idéntico. Si existiera…, lo podrías convencer de ir a la escuela o hacer el trabajo pesado por ti, mientras tú juegas videojuegos o ves televisión. Es un sueño que de seguro todos hemos tenido; y, curiosamente, algo así les sucede a todos los elementos químicos: tienen gemelos.

Seguramente has escuchado sobre los isótopos. Y de inmediato los asocias con radioactividad; uno piensa en Chernóbil y Fukushima. Pero los isótopos son nada más y nada menos que los dobles idénticos de los elementos químicos, pero magnificados. Esto significa que los isótopos de un elemento se comportan de manera casi idéntica al elemento químico (hacen el mismo trabajo), pero son más pesados. Son más gordos que el elemento al que pertenecen porque difieren en la cantidad de neutrones que contienen, poseen más, y en esta diferencia de peso existe un gigantesco mundo de información que todos estos pesados nos pueden proporcionar.

Todos los átomos de un mismo elemento tienen la misma cantidad de protones y electrones. Por ejemplo, el hidrógeno contiene un protón y un electrón, el helio dos, y así, sucesivamente, lo que determina su número atómico. Sin embargo, pueden variar en el número de neutrones. Por ejemplo, el hidrógeno tiene tres isótopos: el protio, sin neutrones —éste es el más flaco—; el deuterio, con un neutrón; y, el tritio, con dos (figura 1). Esto confiere propiedades distintas al mismo elemento, como radioactividad y distinto peso atómico.

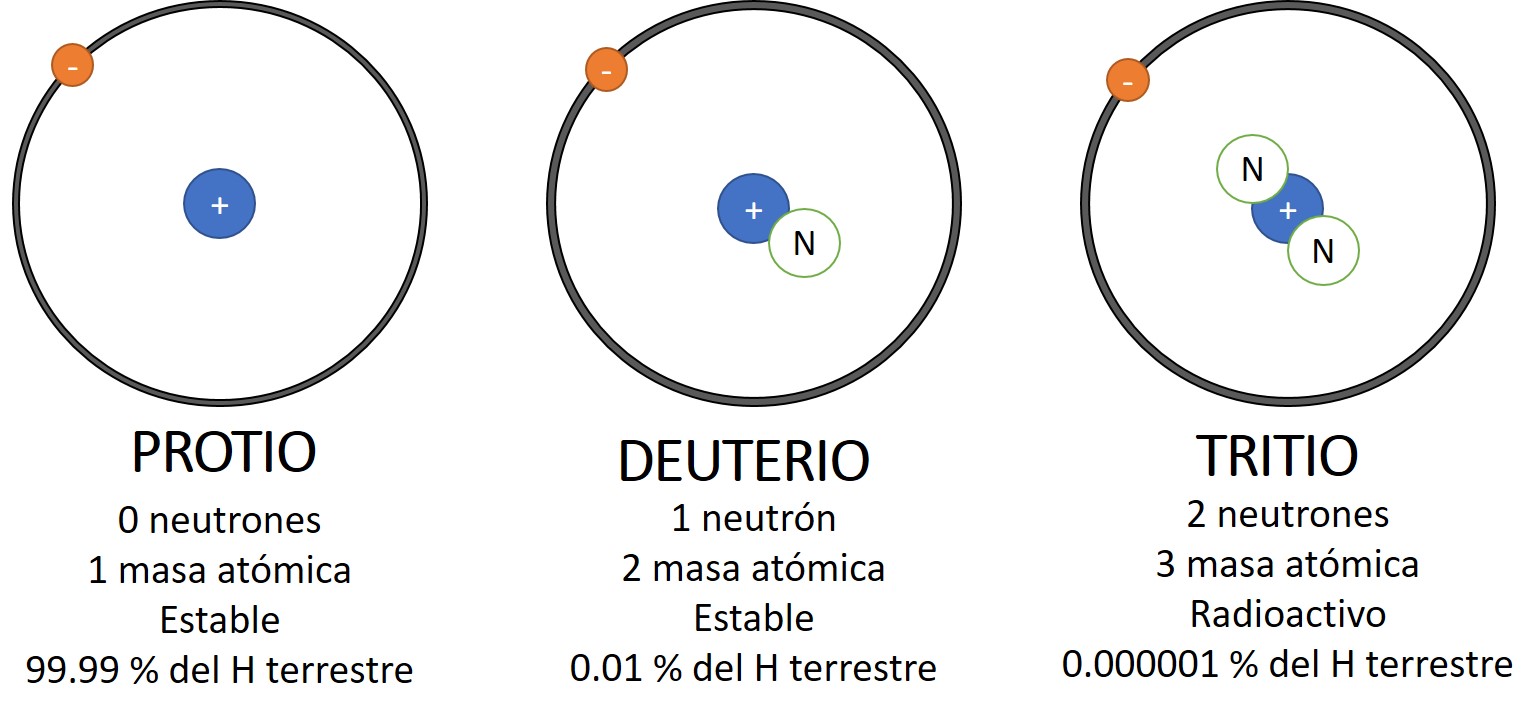
Figura 1. Isótopos de hidrógeno.

Dicha diferencia en sus propiedades tiene importantes implicaciones en distintas ramas de la ciencia. La manera más sencilla de explicarlo es que los isótopos más pesados (con más neutrones) son más difíciles de mover y, por lo tanto, se almacenan con el tiempo. Se acumulan en los planetas, en las distintas capas de la Tierra, en las diferentes formas de vida e incluso en los seres humanos. Entonces, al estudiar los isótopos obtenemos información sobre una nueva cara del universo que nos rodea y los procesos que lo crearon.

Los isótopos en el universo: el origen de la Luna

No todas las estrellas ni todos los planetas están hechos de los mismos elementos. Lo más interesante es que aun aquellos que se parecen tienen una composición isotópica única. Esto quiere decir que mediante la medición de distintos isótopos se puede determinar el origen de un planeta o de un asteroide con relación a su sistema solar. El mejor ejemplo de ello ha sido el estudio del origen de la Luna.

Durante mucho tiempo existieron distintas teorías sobre el origen de la Luna. La primera sugería que se trataba de un planetoide y que la gravedad terrestre la capturó. Otra teoría proponía que ambos cuerpos celestes se formaron al mismo tiempo. Una tercera sostenía que una parte de la Tierra explotó y formó la Luna. Y la última, que la Luna se formó tras el choque de un protoplaneta con la Tierra. Las distintas teorías tenían varios puntos a favor y en contra, lo que causó división entre los astrónomos. Pero fue hasta que las misiones Apolo 15 y Apolo 17 llegaron a la Luna y volvieron que finalmente se pudo determinar de manera casi contundente cuál de todas ellas era la correcta.

Con la llegada a la Luna se pudieron tomar muestras de rocas de su superficie y analizar su composición isotópica. Distintos estudios publicados en las revistas Science y Nature entre 2011 y 2013 mostraron que la composición relativa de los isótopos de titanio, zinc, selenio y oxígeno de la Luna era igual a la de la Tierra. En otras palabras, que tenían el mismo número de átomos gordos y flacos de cada elemento. Esto implica que el origen de nuestro satélite está forzosamente ligado al origen de nuestro planeta y, lo más probable, es que la teoría del gran impacto sea la correcta (figura 2).

Figura 2. Fragmento de roca basáltica lunar. Fuente: Planetary Geology and Lunar Rocks.

Recientemente, Ed Young y colaboradores de UCLA utilizaron un lector de isótopos de alta precisión y lograron determinar que no hay diferencias entre los isótopos de oxígeno en la Tierra y la Luna, lo que los llevó a concluir que el impacto fue causado por un meteorito y el material que salió volando formó el manto de dichos cuerpos celestes. Sus resultados fueron publicados en la revista Science en 2016. El impacto de un cuerpo celeste contra la Tierra en formación también explica la inclinación del eje terrestre y la diferencia en la velocidad de rotación entre la Tierra y la Luna.

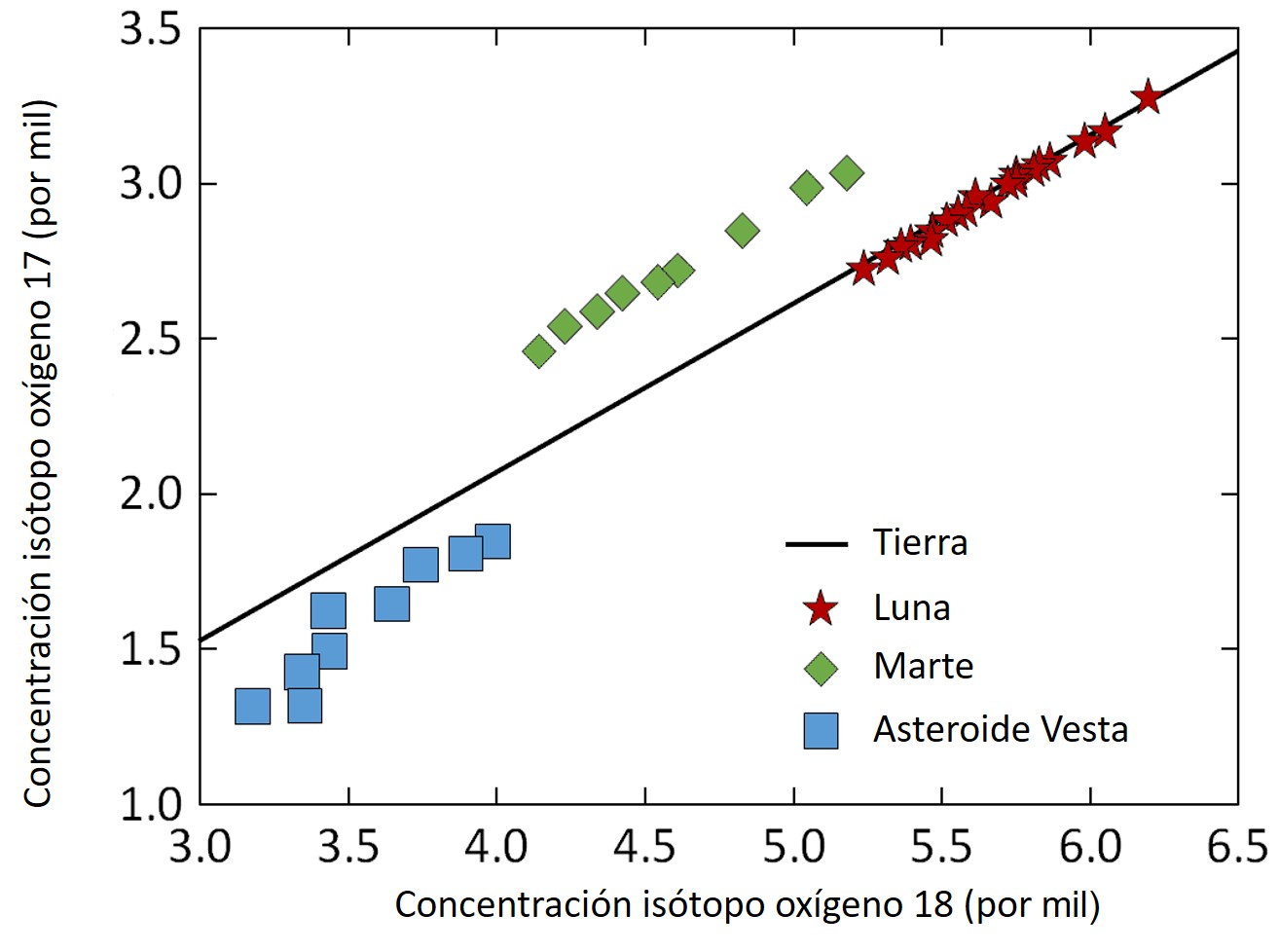
Figura 3. Isótopos de oxígeno en diferentes tipos de rocas. Fuente: modificado de “Oxygen Isotopes and the Moon-Forming Giant Impact”.

Los isótopos para mapear la historia de la Tierra

Una huella efectiva con la que contamos para reconstruir la historia de nuestro planeta es la que van dejado los elementos químicos y sus isótopos. Por ejemplo, los hielos de los casquetes polares de la Antártida y Groenlandia han guardado por milenios toda la información de la historia de la atmósfera y el clima de nuestro planeta. En estos lugares la lluvia cae en forma de nieve y nunca se mezcla con su entorno, dando paso a una columna de precipitaciones históricas.

En el corazón de la Antártida, el lugar más frío de la Tierra, con temperaturas de hasta -90 °C, donde sólo los rusos pudieron construir un centro de investigación, es donde se encuentra la estación de Vostok, y fue allí donde por primera vez se logró perforar el hielo hasta 3 623 metros de profundidad. El cilindro de hielo que se obtuvo reveló información sobre los últimos cuatro ciclos glaciales, es decir, el hielo guardaba la historia de 420 000 años.

En uno de los artículos más leídos en los últimos tiempos, Jean Robert Petit del laboratorio de glaciología y geofísica ambiental del Centre National de la Recherche Scientifique de Francia y colegas de diversas universidades estadounidenses y rusas pudieron describir el clima y la historia de la atmósfera terrestre de los últimos 420 000 años, a partir de estos cilindros. Uno de los análisis consistió en medir los isótopos de oxígeno atrapados en las capas de hielo.

La explicación es que el agua contiene oxígeno 16, pero digamos que también existe un tipo de agua más pesada que contiene un isótopo gordito conocido como oxígeno 18. Esta agua pesada tarda más tiempo en moverse, tiende a evaporarse del mar con mayor dificultad y se adentra menos en los continentes. Estas propiedades aumentan con el frío, pues es más difícil evaporar al oxígeno pesado. Así que la relación entre el oxígeno ligero y el pesado, atrapados en los cilindros de hielo, revela los períodos en los que hubo menor movilidad de agua, principalmente debido a que la temperatura era menor. Usando esta relación como paleo-termómetro se pudieron calcular las temperaturas que había cuando se fueron acumulando las sucesivas capas de nieve. Esto mostró que la temperatura terrestre se había mantenido relativamente estable en todo este tiempo y que un cambio climático como el actual es algo que no se había registrado en el último medio millar de años.

Los isótopos y la vida

El registro que ha dejado la vida en el planeta se ha rastreado para reconstruir su historia con ayuda de los fósiles. Sin embargo, no sólo los dinosaurios o los trilobites han dejado su huella en este planeta, también la han dejado las plantas.

Una de las regiones con mayor belleza natural y al mismo tiempo una de las más inhóspitas y salvajes es la sabana africana, donde los pastizales y los arbustos dominan el paisaje. Pero no siempre fue así, en algún tiempo, hace como veinte millones de años, durante el Mioceno, en esa majestuosa pradera reinaban grandes bosques con árboles de diversas especies.

Se puede decir que los pastos y plantas herbáceas son evolutivamente más novedosos y surgieron durante este período. El cambio de vegetación sucedió por cambios en el clima que provocaron sequías al interior del continente, según encontraron David J. Beerling y Colin P. Osborn de la Universidad de Sheffield, Inglaterra.

¿Cómo llegaron a este descubrimiento? Utilizando isótopos, por supuesto. Las plantas utilizan CO₂ para realizar la fotosíntesis y ellas pueden discriminar entre CO₂ ligero (con carbono 12) y CO₂ pesado (con el gordito carbono 13), y prefieren el carbono ligero. Sin embargo, esta discriminación es distinta entre árboles y hierbas, donde esas últimas tienden a acumular una mayor cantidad de isótopos de carbono 13, más pesado. Este elemento, que la vegetación acumula en las hojas, llega finalmente al suelo donde se descompone y deja su huella isotópica. Así, gracias a la conservación y extracción de suelos de hace millones de años se pudo saber que fue durante el Mioceno cuando los grandes bosques abrieron paso a los primeros pastos, que necesitaban menos agua y soportaban más la radiación.

La historia humana a través de los isótopos

Ahora sabemos que no toda el agua es igual, ni que todas las plantas están hechas de lo mismo. Lo más interesante es que la diferencia entre los isótopos permea a aquellos que se beben el agua o consumen las plantas, incluidos los seres humanos. Entonces, analizando la composición isotópica de fósiles de antiguos humanos e incluso de nuestros ancestros –o de nosotros mismos– se puede entrever el tipo de dieta que éstos tenían y entender más de su estilo de vida.

Por ejemplo, el consumo de frutas, raíces y tubérculos genera marcas isotópicas de carbono diferentes a las que se obtienen al comer cereales o comer pescado. Al analizar distintos dientes del registro fósil humano, Richard Klein de la Universidad de Standford, utilizando isótopos de carbono y nitrógeno, encontró que, en general, los Australopithecus afarensis que vivieron en África hace cuatro millones de años tenían una dieta basada en frutas, más parecida a la de los chimpancés actuales. Sin embargo, los primeros Homo (erectus y sapiens) consumían una mayor proporción de granos y carne (35% de su dieta, hace dos millones de años), misma que aumentó al pasar el tiempo (hasta 80% hace un millón y medio de años). Esta diferencia en las dietas y la mayor ingesta de proteínas es una de las posibles razones por las cuales nuestro cerebro pudo desarrollarse a mayor velocidad que el de otros primates que sólo se alimentan de frutas.

Otro ejemplo interesante nos lo dan los isótopos del nitrógeno. En general, los peces tienen una composición de dicho elemento distinta a la de los animales terrestres; con lo cual, los seres humanos cuya dieta sea principalmente marina también mostrarán una señal isotópica distintiva. En un artículo, publicado hace casi treinta y cinco años (1983) en la revista Science, Margaret Schoeninger y colaboradores analizaron el registro fósil de los pobladores de América de hace diez mil años. Los resultados mostraron claramente que las civilizaciones de Norteamérica, como los esquimales, dependían fuertemente del consumo de pescado y animales marinos para su supervivencia; al contrario, las culturas más cercanas al Ecuador basaban su alimentación en plantas terrestres.

Pero los isótopos también pueden ser utilizados para distinguir entre la dieta de personas aún vivas. Por ejemplo, el cabello de los vegetarianos tiene hasta 3% menos nitrógeno pesado que el de los que sí comen carne, y el de los veganos hasta 6% menos (ver figura 4). Asimismo, el agua de distintas partes del mundo tiene diferentes concentraciones de selenio pesado, por lo que analizando el cabello de una persona se puede determinar de qué parte del mundo proviene. Esto es particularmente importante en las ciencias forenses, donde el estudio de la composición isotópica de una persona puede proporcionar información relevante de su estilo de vida y origen.

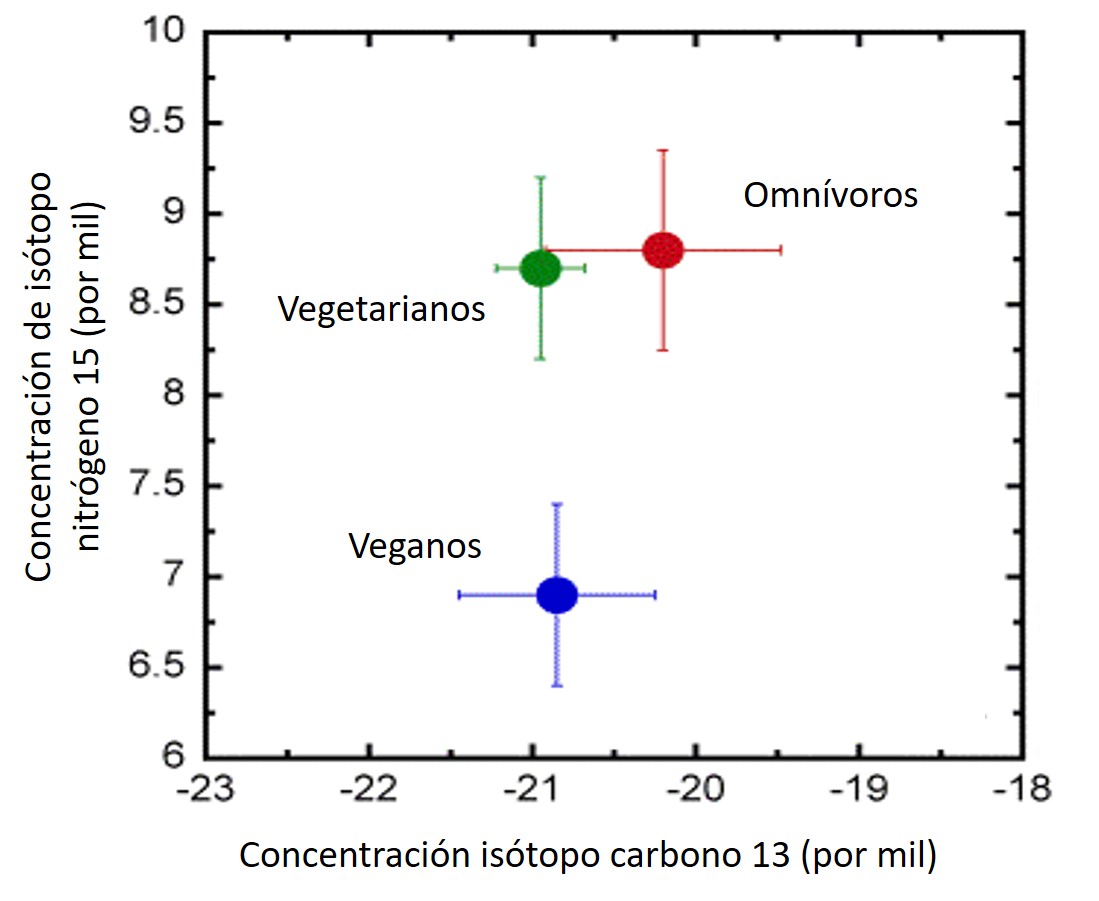
Figura 4. Isótopos de los cabellos humanos según el tipo de dieta.

Medicina nuclear

Pero los isótopos tienen otros usos. Además de ayudarnos a entender eventos históricos, también sirven para detectar y tratar enfermedades. Esta rama de la medicina se conoce como medicina nuclear y tuvo sus orígenes en los últimos cincuenta años. Sus principios se basan en inyectar o absorber de manera oral isótopos radiactivos de algún elemento en particular, por ejemplo, yodo, y mediante el uso de radiografías o tomografías seguir su flujo a través del cuerpo humano. Esto permite detectar de manera fácil y no invasiva la presencia de un sinnúmero de padecimientos como cálculos en la vesícula, problemas cardíacos, infecciones en los huesos y más comúnmente distintos tipos de cáncer. Si bien existen algunos riesgos al inyectar elementos radioactivos en el cuerpo, éstos son en general inocuos y los procedimientos son altamente benéficos para determinar y tratar enfermedades crónicas de manera temprana.

Pero no sólo se utilizan para detectar enfermedades, sino también para tratarlas. Por ejemplo, la administración de yodo radiactivo (yodo 123) es común para el tratamiento de cáncer de tiroides, o los isótopos de samario y estroncio que se utilizan para el tratamiento de cáncer de huesos y de pulmones. Esto tiene cierta ventaja sobre otros métodos de quimioterapia, pues la radiación que se emite es muy localizada, y así se minimizan los efectos secundarios.

Ciencia por descubrir

Existen otras muchas aplicaciones del estudio de los isótopos; por ejemplo, la determinación del origen del plomo utilizado en balas o explosivos, el estudio del origen de los meteoritos a partir de isótopos de iridio, entre otras. Sin embargo, hay muchos elementos y sus respectivos isótopos que aún no han sido explorados. Por ejemplo, el estaño tiene cerca de diez distintos isótopos por estudiar.

Hay todo un mundo de posibilidades por investigar, quién sabe qué otras maravillas interesantes descubriremos en el futuro a partir de las diferencias en unos pocos neutrones. ¿Quién diría que los gorditos de la naturaleza nos darían tanto de que hablar?

Referencias

• Canpu, R. (2012). Forming a Moon with an Earth-like Composition via a Giant Impact. Science, 23(6110), 1052-1055. DOI: https://doi.org/10.1126/science.1226073.
• Elkins-Tanton, L. (2013). Planetary science: Occam’s origin of the Moon. Nature Geosciences, 6, 996–998. DOI: https://doi.org/10.1038/ngeo2026.
• Young, E. D., Kohl, I. E., Warren, P. H., Rubie, D. C., Jacobson, S. A. y Morbidelli, A. (2016). Oxygen isotopic evidence for vigorous mixing during the Moon-forming giant impact. Science, 351(6272), 493-496. DOI: https://doi.org/10.1126/science.aad0525.
• Petit, J. R., Jouzel, J., Raynaud, D., Barkov, N. I., Barnola, J. M., Basile, I. et al. (1999). Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature, 399(6735), 429. DOI: https://doi.org/10.1038/20859.
• Beerling, D. J. y Osborne, C. P. (2006). The origin of the savanna biome. Global change biology, 12(11), 2023-2031. DOI: https://doi.org/10.1111/j.1365-2486.2006.01239.x.
• Klein, R. G. (2013). Stable carbon isotopes and human evolution. Proceedings of the National Academy of Sciences, 110(26), 10470-10472. DOI: https://doi.org/10.1073/pnas.1307308110.
• Schoeninger, M. J., DeNiro, M. J. y Tauber, H. (1983). Stable nitrogen isotope ratios of bone collagen reflect marine and terrestrial components of prehistoric human diet. Science, 220(4604), 1381-1383. DOI: https://doi.org/10.1126/science.6344217.

Recepción: 6/3/2018. Aprobación: 8/8/2018.

Resumen

El número π es de mucha utilidad en diversas ramas de la ciencia y la ingeniería y este ha sido usado desde hace milenios en el desarrollo de infraestructuras de ciudades, construcción de puentes, cálculos de distancias y otras cantidades; sin embargo, existen aún muchas incógnitas que, si bien se asumen verdaderas por comprobaciones numéricas de casos particulares, no se han logrado demostrar. En este artículo se hará una revisión sobre la historia del número π, incluyendo el famoso problema de la cuadratura del círculo con el fin de entender algunas de sus características, para finalmente revisar algunos de los problemas que aún siguen abiertos.
Palabras clave: Número pi, números irracionales, números normales, series.

Mysteries of number π

Abstract

The π number is very useful in various branches of science and technology and it has been used for millennia in the development of city infrastructures, bridge construction, distance measures and other measurements. However, there are still many questions that although they are assumed to be true by numerical checks of particular cases, they have not been proven. In this article we will review the history of the π number, including the famous quadrature of the circle problem with the objective to understand some of the characteristics of number π, to finally review some of the problems that are still open.
Keywords: Number pi, irrational numbers, normal numbers, series.

Introducción

Durante la educación básica, en matemáticas, los niños aprendes a calcular el área de diferentes “figuras geométricas”, por ejemplo: cuadrados, rectángulos y círculos. Estos cálculos son útiles debido a las diversas aplicaciones en la vida cotidiana, como saber el tamaño de una superficie, por mencionar una.

La primera área que se aprende a calcular es la del cuadrado que es simplemente el cuadrado (es decir, la multiplicación del número por sí mismo) de la longitud de su lado $(área=l^2)$. Esta fórmula es tan intuitiva que no requiere de una demostración y la aceptamos como la definición.

Para otras figuras, calculamos su área por la suma de las áreas de cuadrados pequeños que la cubren. Así, dividiendo un rectángulo en pequeños cuadrados, es fácil ver que el área total de este será: $área=bxh$, dónde $b$ es la longitud de la base del rectángulo y $h$ su altura.

Otras fórmulas que se estudian son aquellas con las que se calculan las áreas del triángulo, el rombo, el trapezoide y el círculo. El caso del círculo aparece una “extraña” constante, $\mathrm{\pi }=3.14$. La fórmula para estimar el área de éstos es: $\mathrm{área}={\mathrm{\pi r}}^2$, donde r es el radio del círculo. Por lo regular no se explica de dónde sale esta ecuación, lo único que se enseña es que π es el valor de la circunferencia1 de un círculo de radio 1, la cual se puede medir dibujando un círculo con un compás y midiendo la longitud de un hilo que cubra la circunferencia. La relación entre el área de un círculo y su diámetro se puede entender si se aproxima al círculo por polígonos regulares de muchos lados. En este caso, el área del círculo es aproximadamente el área del polígono (ver figura 1a), mientras que su perímetro es aproximadamente la suma de los de los lados.

El polígono se puede dividir en tantos triángulos isósceles como lados tenga. Si se acomodan adecuadamente estos triángulos, podemos calcular el área del polígono como lo haríamos con la de un rectángulo cuya base es aproximadamente $\mathrm{r}$ y la altura es la mitad del perímetro del polígono que, a su vez, es más o menos la mitad del perímetro del círculo (ver figura 2b), es decir $\mathrm{\pi r}$. Al multiplicar la base ($~\mathrm{r}$) por la altura ($~\mathrm{\pi r}$) de este rectángulo obtenemos su área, que es el área del polígono que a su vez es aproximadamente el área de un círculo (${\mathrm{\pi r}}^2$).

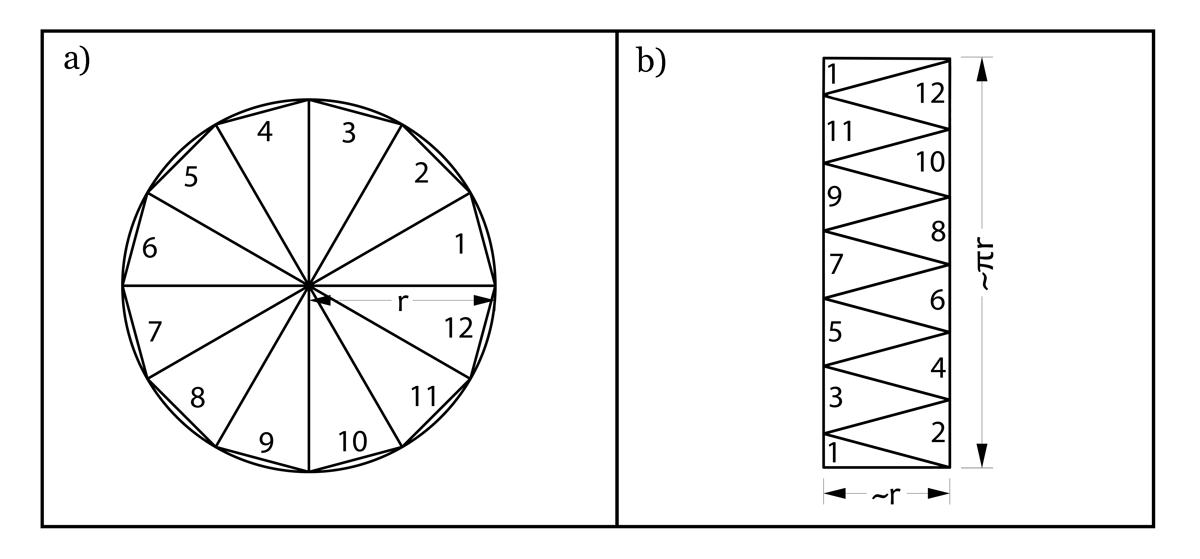
Figura 1. Esquema de la demostración de que el área de un círculo es πr². En (a) el círculo ha sido aproximado por un polígono de 12 lados. Este polígono está compuesto por 12 triángulos isósceles iguales. En (b) Los mismos 12 triángulos han sido acomodados para formar un rectángulo de base ~r y altura ~πr.

Cuadratura del círculo

El primer método del que hablamos para estimar π (el que usa un hilo) mide directamente la circunferencia, la cual podemos dibujar con un compás. El problema de este método es la dificultad representa la precisión al medir la longitud del hilo, ésta se incrementa si el tamaño de la circunferencia es mayor, el problema es que entre más grandes son los círculos, es más difícil dibujarlos y por lo tanto poco precisos. Por esta razón, la mayoría de las culturas en la antigüedad hicieron estimaciones inexactas; casi siempre consideraban $\mathrm{\pi }=3$.

Medir el área de un cuadrado suele ser más sencillo que medir el área o perímetro de un círculo y por lo tanto también suele ser más preciso.; por ello, podríamos pensar que un mejor método sería medir el área de un cuadrado de lado $|=\sqrt{\pi }$. El problema de este método es dibujar un cuadrado con esa característica. Para trazar figuras geométricas con mucha precisión, los dos instrumentos por excelencia son el compás y la regla.2 Entonces, primero debemos preguntarnos ¿Cómo construir, con regla y compás un cuadrado cuya área sea la de un círculo de radio 1?, de tal manera que medir su área sea medir π. A este problema se le conoce como la cuadratura del círculo y su solución no es para nada intuitiva;3 tanto así, que se convirtió en uno de los problemas más desafiantes en la historia de las matemáticas. Los primeros en tener avances significativos al respecto fueron los egipcios (Petrie, 1940), 1800 años a.C. Ellos descubrieron que el cuadrado que medía 16/9 de unidades por lado tenía un área muy similar al de un círculo de radio 1.4 Con esto aproximaron la constante π como $\mathrm{\pi }=\frac{256}{81}~3.16$, la cual se volvió una de las mejores aproximaciones de la antigüedad y cuyo descubrimiento tardó más de mil años en ser rebasado.

A lo largo de la historia hubo miles de intentos por resolver la cuadratura del círculo y un sinfín de propuestas sobre cómo construir (erróneamente) un cuadrado con área igual a la de un círculo dado. No fue sino hasta 1882, que el matemático alemán Lindermann logró resolver el misterio al demostrar la imposibilidad de dicha construcción; es decir, el problema se mantuvo abierto por más de 3 mil años, uno de los problemas matemáticos que más tiempo han estado sin resolverse. Como éste duró tanto tiempo sin solución, adquirió fama y llamó la atención de matemáticos aficionados. Hay publicaciones que tratan de demostrar, de forma errónea, las cuadraturas del círculo, al menos hasta 1894 (Goodwin, 1894).

Aproximación de Arquímides

Desde el trabajo plasmado en el papiro de Rhind, donde se muestra la aproximación a π como 3.16, no hubo avances sustanciales en esta constante, sino hasta la época de Arquímides (Arndt y Haenel, 2001), quien alrededor del año 250 a.C. aproximó el perímetro del círculo de diámetro 1 mediante polígonos, tal como se muestra en la figura 2a, tomando tanto la aproximación inferior, como la aproximación superior. El algoritmo de Arquímides dio pie a una serie de mejoras en la aproximación de π que llegó hasta 16 dígitos decimales de precisión para el año 1593 por Adrianus Romanus (Schepler, 1950). Por la importancia del cálculo de Arquímides, se explicará brevemente la aproximación inferior, aunque ello requiere de un esfuerzo mental elevado.

Primero notamos que si uno construye un hexágono inscrito en un círculo (dentro del círculo, pero cuyos vértices forman parte de la circunferencia), podemos dividir éste en 6 triángulos equiláteros (ver figura 2), cuyo lado es un radio, por lo tanto, el perímetro del hexágono será simplemente $6r_{}$. Si $r=\frac{1}{2}$, el perímetro será 3, que es nuestra primera aproximación de π. La siguiente aproximación, consiste en pasar a un polígono de 12 lados. Para esto, sobre cada uno de los lados del hexágono insertamos un triángulo isósceles, cuya base sea un lado del hexágono que llamaremos $l_6=r$ de forma que el otro vértice quede sobre la circunferencia. Como el triángulo es isósceles, cada uno de los lados de la envolvente será del mismo tamaño, formando un polígono regular de 12 lados. Sabemos que la distancia del centro de la circunferencia a cualquiera de los vértices de nuestro polígono es un radio. Por lo tanto, la altura del triángulo isósceles será simplemente $h_{12}=r–L_6$, donde $L_6$ es la apotema del hexágono (la distancia del centro del círculo al centro de uno de los lados del hexágono). Para calcular $L_6$ podemos usar el Teorema de Pitágoras, obteniendo $L_6=\sqrt{r^2–\frac{1}{4}{r}^2}=\sqrt{3}\frac{r}{2}$. Una vez más usamos este teorema para calcular el lado $l_{12}$ del polígono de 12 lados, pues tenemos la altura $h_{12}$ del triángulo isósceles y su base $l_6=r$, por lo tanto $l_{12}=\sqrt{\raisebox{1ex}{$l_{26}$}\!\left/ \!\raisebox{-1ex}{$4$}\right.+h_{12}^2}$. Repetimos este proceso una y otra vez simplemente sustituyendo $l_6$ por $l_{3\times 2}n$ para después calcular $L_{3\times 2^n}$, $h_{6\times 2^n}$ y finalmente $l_{6\times 2^n}$.

Arquímides repitió este procedimiento 4 veces y obtuvo primero el polígono de 12 lados, después de 24, 48 y finalmente 96 lados. Aproximando las raíces cuadradas que obtenía por fracciones, pudo demostrar que $\mathrm{\pi }>\frac{223}{71}$ y ya antes había mostrado, usando un procedimiento similar, pero con polígonos circunscritos (por fuera de la circunferencia), que $\mathrm{\pi }<\frac{22}{7}$. Es decir, pudo acotar el valor de π entre $\frac{223}{71}$ y $\frac{22}{7}$, lo cual mejoró la aproximación de los egipcios; pero, más importante aún, creó un algoritmo con el que en principio podía aproximarse tanto como se quisiera el valor de π.

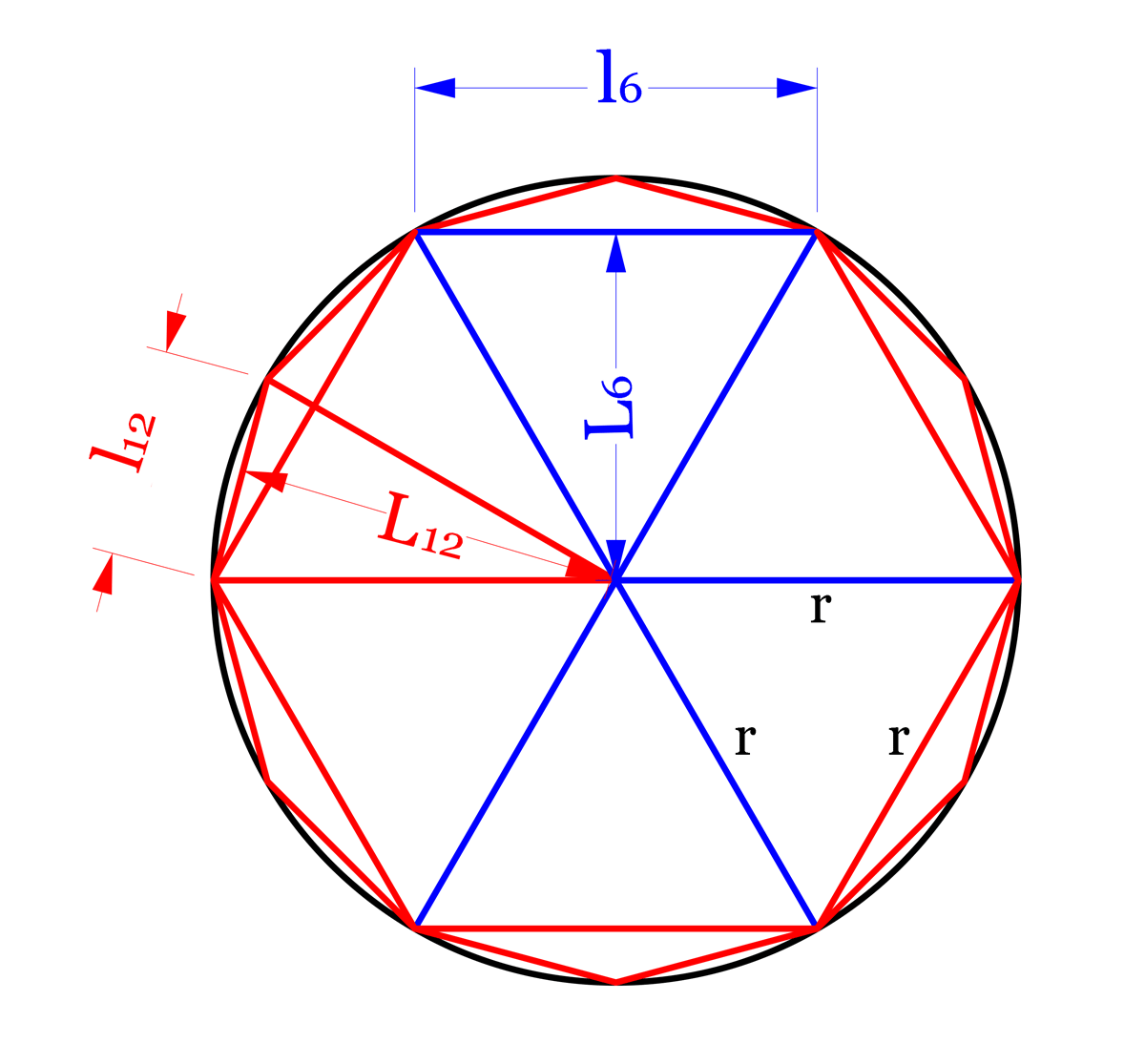
Figura 2. Esquema para desarrollar el algoritmo de Arquímides para el cálculo de π.

Otras definiciones de π

Después de Arquímides hubo muchos matemáticos que intentaron crear mejores algoritmos para calcular π a través de muchos esfuerzos por modificar la definición de la constante, mostrando equivalencias con la definición original. Hay un sinfín de posibles definiciones de π, cada una de ellas relacionada con alguna fórmula matemática o física importante. Mencionaremos sólo algunas de ellas.

Una interesante definición se la debemos a Euler (Posamentier y Lehmann, 2004), quien encontró que la probabilidad de que dos números naturales cualesquiera sean primos relativos5 está dada por $p=\frac{6}{n^2}$, con lo que se pudo definir más tarde a la constante en función de la probabilidad de que dos números sean primos relativos $\mathrm{\pi }=\sqrt{\frac{6}{\mathrm{p}}}$. La belleza de esta definición es que involucra 2 ramas de las matemáticas, la probabilidad y la teoría de los números.

Otras definiciones importantes en el cálculo numérico de π son las que contienen las funciones trigonométricas. Por ejemplo, usando el resultado de $tan\left(\frac{\mathrm{\pi }}{4}\right)=1$ se puede definir $\mathrm{\pi }=4arctan\left(1\right)$. No entraremos en detalle, pero se puede mostrar que con herramientas de cálculo6 y la definición que acabamos de dar que $\mathrm{\pi }=1+\frac{1}{1}+\frac{1}{3}+\frac{1}{5}+\cdots +\frac{1}{(2n+1)}$… Mediante el uso de esta serie, se pueden llegar a precisiones del número π tan grandes como se quiera de forma relativamente rápida con ayuda de computadoras modernas; por ejemplo, hasta noviembre del 2016, el récord en cifras de π era de 22,459,157,718,361 cifras de precisión. El cálculo se puede revisar en: http://www.numberworld.org/y-cruncher/.

Irracionalidad de π

Mejorar la precisión de π llevó a preguntarse si en su expresión decimal no habría una secuencia de números que se repitiera periódicamente como sucede en los números racionales. Por ejemplo, el número 1/3 se puede escribir como 0.33333… repitiendo periódicamente el número 3, o el número 1/7 = 0.142857142857… repitiendo la cadena de cifras “142857” de forma periódica. Si π tuviera una expresión así, sería entonces un número racional, es decir, se podría expresar como una fracción de números enteros (como $\frac{223}{71}$).

La pregunta respecto a la racionalidad de π, fue otro de los grandes problemas en la historia de las matemáticas y tardó algunos siglos en se respondida. En 1761 el matemático francoalemán Johann Lambert (Lambert, 2004), fue el primero en demostrar que el número π no se puede expresar como una fracción, es decir, es irracional. La prueba de Lambert consistió en escribir $tan\left(x\right)$ en la forma: $tan\left(x\right)=a_{0}x+1/(a_{1}x+1/(a_{2}x+1/\left(a_{3}x+..\left)\right)\right)$, donde todos los $a_{\mathit{i}}$ son enteros excepto, quizá, el primero que puede ser una fracción. Finalmente mostrar que si $x$ es un número racional, entonces la fracción tiene una expresión infinita (hay una infinidad de valores de $a_{\mathit{i}}$ diferentes de 0) pero $tan\left(\frac{\mathrm{\pi }}{4}\right)=1$ y 1 es naturalmente una fracción continua finita por ser un entero. Lo que implica que $\frac{\mathrm{\pi }}{4}$ no puede ser un número racional (si lo fuera, la fracción continua no podría ser finita), por lo tanto π tiene que ser irracional.

En general, cualquier número irracional se puede aproximar por números racionales tan bien como queramos. Por eso π se podría aproximar tanto como queramos por una fracción; pero ¿hay alguna forma de medir qué tan bien aproxima un número racional a uno irracional (en particular π)? En 1891, el matemático alemán Adolf Hurwitz (Hurwitz, 1891) demostró que dado un número irracional ψ, existen infinitos números p y q primos relativos (sin divisores comunes) entre sí, de tal forma que: $\left|\begin{array}{cc}\psi & –\frac{p}{q}\end{array}\right|<\frac{1}{\sqrt{5q^2}}$, es decir, el error en la mejor de las aproximaciones es menor que $\frac{1}{\sqrt{5q^2}}$. Por ejemplo, sabemos que 22/7 es una buena aproximación a π puesto que cumple con la desigualdad arriba mencionada, es decir, el error es menor que $\frac{1}{\sqrt{5q^2}}\approx 0.00913$. La desigualdad de Hurwitz, tiene una sola constante, $\sqrt{5}$. Uno podría preguntarse qué sucede si en vez de $\sqrt{5}$ pusiéramos un número más grande, por ejemplo 10 ¿seguiría siendo válida la desigualdad? La respuesta es que para algunos números irracionales esta desigualdad seguirá siendo válida para infinitos valores de q, pero para otros números irracionales no. En particular, para el número dorado $\phi =\frac{(1+\sqrt{5})}{2}\approx 1.618$, la constante más grande que se puede poner es $\sqrt{5}$, pero para otros números irracionales la constante puede ser mayor.

Lo anterior nos lleva a preguntarnos por el grado de irracionalidad de los números, el cual podría medirse calculando el valor de la constante más grande que se puede poner multiplicando a $q$ en la desigualdad de Hurwitz. Entre mayor sea la constante “menos irracional” es el número. Pero se ha descubierto que hay muchos números cuya constante es el infinito. En ese caso, la fórmula de Hurwitz se puede sustituir por $\left|\begin{array}{cc}\psi & –\frac{p}{q}\end{array}\right|<q^{–\alpha }$ con α un número mayor o igual que 2. Se define entonces a α como el grado de irracionalidad de un número. Entre más grande, menos irracional es el número.

El físico y matemático francés Liuville (Wells, 1997) mostró que existen números irracionales (hoy conocidos como números de Liuville) que tienen la propiedad de aproximarse tan rápidamente mediante números racionales que α=∞. Se ha probado que los números algebráicos (los que son solución de una ecuación polinomial, por ejemplo, solución de $6x^5–2x^2+1=3$), son “muy” irracionales, en el sentido de que su grado de irracionalidad es 2, siendo los más irracionales de todos los números.7 Si el número π fuera un número algebraico, sería entonces un número muy irracional.

Volviendo al tema de la cuadratura del círculo, en 1843, el matemático y físico francés Joseph Liuville revisó los manuscritos de Evariste Galois (Liouville, 1846 y Neuenschwander, 1989), quien en 1831 habría escrito, poco antes de morir en un duelo, la demostración sobre la imposibilidad de construir cualquier segmento de longitud que no sea un número algebraico (a estos números se les llama trascendentales). De esta forma, si π fuera algebraico cabría la posibilidad de que se pudiera cuadrar el círculo, y su grado de irracionalidad sería 2, mientras que si fuera trascendental (no algebraico), entonces no se podría cuadrar el círculo (pues si π es trascendental, también lo es $\sqrt{\mathrm{\pi }}$) pero a cambio quedaría abierta la pregunta sobre el grado de irracionalidad de π. En 1882, el matemático alemán Ferdinand Lindermann (Lindermann, 1882) demostró que π es un número no algebraico y con ello se concluyó que no se puede cuadrar el círculo, sin embargo, abrió la posibilidad a que el grado de irracionalidad de π sea mayor a 2.

Medir el grado de irracionalidad de π es importante porque nos podría dar pista sobre cuál es la mejor forma de aproximar este número sin la necesidad de guardar tantas cifras decimales que ocupan mucha memoria. Por otro lado, en 1963 los físicos y matemáticos Kolmogorov, Arnold y Mosel (Arnold, 1963) hicieron una teoría matemática sobre la estabilidad de sistemas no lineales (sistemas dinámicos en el que el cambio en la respuesta del sistema a un estímulo no es proporcional a ese mismo estímulo). Para entender el resultado de estos 3 personajes, vale la pena hacer experimento imaginario. Supongamos que tenemos un péndulo doble como el de la figura 3. Si movemos adecuadamente el péndulo impulsándolo desde abajo, el sistema oscilará tal como oscila un péndulo de un reloj. Sin embargo, si golpeamos (perturbamos) el péndulo de arriba, el movimiento del sistema compuesto pasará a ser caótico (impredecible). Qué tan fuerte tenemos que golpear al péndulo para volverlo caótico depende del grado de irracionalidad de $\raisebox{1ex}{$l_1$}\!\left/ \!\raisebox{-1ex}{$l_2$}\right.$, la razón entre la longitud del primer péndulo y la longitud del segundo. Así, conocer el grado de irracionalidad de un número nos puede dar pista sobre qué tan estables son ciertos sistemas. Puesto que el número π es muy frecuente en la naturaleza, nos interesa saber qué tan irracional es.

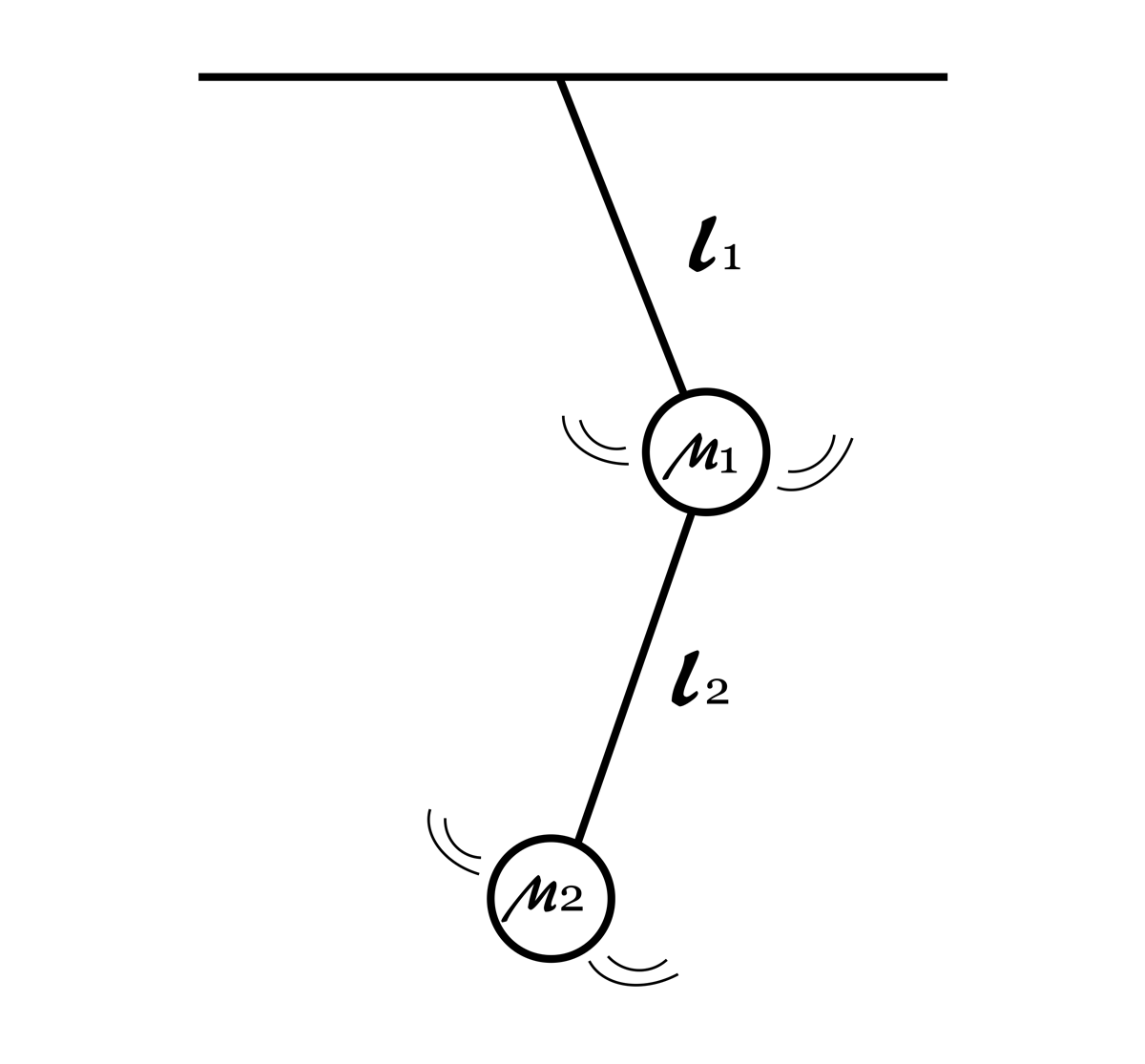
Figura 3. Esquema de un péndulo doble.

Hoy en día se tienen relativamente pocos avances para saber el grado de irracionalidad de π, la mayoría de estos avances son cálculos numéricos; sin embargo, dada la dificultad para medir el exponente, la precisión numérica que se tiene sobre el grado de irracionalidad sigue siendo bastante mala. Analíticamente, Salikhov logró acotar el grado de irracionalidad de π por α$<7.6063$ (Salikhov 2010), sin embargo, las estimaciones numéricas parecen mostrar que este exponente es más bien cercano a 2.

Primer problema abierto: ¿Cuánto vale el grado de irracionalidad de π? En un esfuerzo por mejorar la cota del exponente, Alekseyev (2011) conjeturó que la serie: $\sum _{n=1}^{\infty }\frac{1}{n^3{\sin }^2\left(n\right)}$ es convergente, y con ello logró mostrar que si su conjetura es verdadera, entonces el grado de irracionalidad de π tiene que ser menor que 2.5, lo cual mejora mucho la cota del grado de irracionalidad de π; sin embargo, sigue abierto el problema sobre la convergencia de la serie. Por eso, un problema quizá más sencillo a resolverse es verificar la convergencia de esta serie. Segundo problema abierto: Demostrar que la serie $\sum _{n=1}^{\infty }\frac{1}{n^3{\sin }^2\left(n\right)}$ es o no convergente.

Normalidad de π

Como dijimos previamente, parte del interés en medir el grado de irracionalidad de π es encontrar una forma compacta de aproximar esta constante. Otra forma sería encontrar una estructura en las cifras del desarrollo decimal de π. Por ejemplo, el número 1.234567891011… es un número irracional cuya estructura es bastante clara y, por lo tanto, agregar cifras decimales a su desarrollo resulta sumamente fácil. Por otro lado, resulta fascinante en sí entender la estructura de las cifras en el desarrollo decimal de un número, de alguna forma nos arroja información sobre la naturaleza misma de éste y por lo tanto nos da información sobre la naturaleza de los problemas donde aparece π.

¿Existirá una estructura similar al de 1.234567… en π de forma oculta? Esta pregunta es la que sugiere el cineasta Darren Aronovsky en su película Pi, el orden del caos, donde el protagonista es un matemático que busca secuencias dentro del desarrollo decimal de π. Si no tuviera ninguna estructura, sería entonces un desarrollo desordenado de números, como si se hubiera construido lanzando números al azar. Si este fuera el caso, entonces las cadenas de cifras deberían estar distribuidas de forma homogénea (a veces se dice de forma normal). Cuando un número tiene una distribución homogénea de cifras se dice que el número es normal. Una buena pregunta es entonces si π es un número normal. Si π fuera normal, entonces podríamos usar sus cifras como un generador de números aleatorios.

Tercer problema abierto: ¿Es π un número normal? Sobre este problema realmente no hay muchos avances al respecto, excepto por revisiones numéricas, donde todo parece indicar que las cifras 0-9 aparecen todas con una distribución homogénea (la probabilidad de seleccionar una cifra dada es 1/10). Más aún, se han hecho estudios sobre cadenas de algunas cuantas cifras y hasta ahora pareciera que la probabilidad de tener una cadena de n cifras es $\frac{1}{{10}^n}$ tal como se esperaría si π fuera un número normal; pero de hecho no se sabe ni siquiera si cualquier cadena de números aparece dentro del desarrollo decimal de π.

Esto nos lleva a un problema más sencillo con respecto de la normalidad de π, pero que tampoco se ha resuelto, nuestro cuarto y último misterio sin resolver: Problema abierto 4: ¿Aparecen todas las cadenas de cifras en el desarrollo decimal de π?

Una curiosidad es que existen algunas páginas en internet donde es posible buscar dentro de los primeros cientos (o miles) de cifras de π, una cadena dada, por ejemplo, tu fecha de cumpleaños en el formato: ddmmaaaa, que consta de 8 cifras. En algunos casos se usa la versión corta de fechas dd-mm-aa, donde sólo se usan 6 cifras, es decir, si π es normal, uno de cada millón de cifras contiene tu fecha reducida de cumpleaños aproximadamente.

¿Por qué estudiar π?

Para terminar este texto quiero hacer una reflexión sobre qué importancia tiene conocer si existe cualquier cadena dentro del desarrollo de π. La primera respuesta que podría argumentar es que muchos conocimientos en la ciencia y en particular en las matemáticas han encontrado aplicación decenas o incluso cientos de años después de ser descubiertos y éste podría ser el caso a estos problemas. Por otro lado, hay una estética detrás de π y eso será, para muchos, motivación suficiente para estudiar sus propiedades; después de todo, si disfrutamos entender un proceso, es justificación suficiente para estudiarlo; sin embargo, existen otros motivos para interesarse en las propiedades de π.

Tanto en matemáticas, como en física, π aparece una y otra vez en diversas ecuaciones. En física está presente en las ecuaciones de Maxwell, en el principio de incertidumbre de Heisenberg, en el periodo del péndulo, etcétera. Mientras que en matemáticas está en la probabilidad de que dos números enteros sean primos relativos, en la distribución gaussiana, en desarrollos de Fourier, etcétera. Esto nos dice un poco sobre la importancia que tiene esta constante, por eso, entender sus propiedades es de sumo interés. Al estudiar las propiedades de π de cierta forma logramos comprender que, si hay una función periódica, o hay azar en un proceso, probablemente aparecerá π. De forma inversa, si encontramos π en alguna ecuación o medición, probablemente estará relacionado con una periodicidad o un proceso azaroso. Además, cuando se trata de algo isotrópico, es decir, cuando el comportamiento es el mismo en todas direcciones, aparece nuevamente π por tratarse entonces de algo radial, es decir, sobre una esfera, donde cada capa sigue las mismas reglas. Entender las propiedades de π nos puede llevar a descubrir otra clase de procesos donde la constante podría aparecer. ¿Por qué nos interesamos en π y no otras constantes? Porque sí nos interesamos también en otras constantes, aunque es verdad que hay algunas que son más importantes que otras por la frecuencia con la que las encontramos en la naturaleza, π es una de las más frecuentes y me atrevería a decir que es quizá la más frecuente de las constantes quitando el 0 y el 1.

Este artículo está basado en la plática que dio el autor con el nombre “problemas abiertos acerca de pi” en el marco de la celebración del Día de Pi 2018 organizado por el SUMEN.

Agradecimientos

Agradezco el apoyo de Cedrela Loera tanto con correcciones de estilo, como con las imágenes proporcionadas.

Referencias

• Malisani, E. (1987) Construcción del pentágono regular con sólo compás. Revista de Educación Matemática, 3(2).
• Petrie, W. M. F. (1940). Wisdom of the Egyptians: With 128 Figures (Vol. 63). British school of archaeology in Egypt and B. Quaritch Limited, London, UK. Nota: El libro hace referencia al papiro de Rhind, que se puede consultar en: http://www.britishmuseum.org/research/collection_online/collection_object_details.aspx?objectId=110036&partId=1.
• Lindemann, F. (1882). Über die Zahl π.*. Mathematische Annalen, 20(2), 213-225.
• Goodwin, E. J. (1894). Quadrature of the circle. Amer. Math. Monthly, 1, 246-247.
• Arndt, J., y Haenel, C. (2001). Pi-unleashed. Springer Science & Business Media. p.170.
• Schepler, H. C. (1950). The chronology of pi. Mathematics Magazine, 23(4), 216-228.
• Posamentier, A. S., & Lehmann, I. (2004). Pi: a biography of the world’s most mysterious number. Prometheus Books, New York, NY.
• Lambert, M. (2004). Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques. In Pi: A Source Book (pp. 129-140). Springer, New York, NY.
• Hurwitz, A. (1891). Über die angenäherte Darstellung der Irrationalzahlen durch rationale Brüche. Mathematische Annalen, 39(2), 279-284.
• Wells, D. (1997). The Penguin dictionary of curious and interesting numbers. Penguin. London, UK.
• Liouville, J. (1846). Oeuvres Mathématiques d’Évariste Galois. Journal de Mathématiques pures et appliquées, 11, 381-384.
• Neuenschwander, E. (1989). The unpublished papers of Joseph Liouville in Bordeaux. Historia mathematica, 16(4), 334-342.
• Arnold, V. I. (1963). d, Proof of a theorem of AN Kolmogorov on the preservation of conditionally periodic motions under a small perturbation of the Hamiltonian, Uspehi Mat. Nauk, 18, 13-40.
• Salikhov, V. K. (2010). On the measure of irrationality of the number π. Mathematical Notes, 88(3), 563-573. Alekseyev, M. A. (2011). On convergence of the Flint Hills series. arXiv preprint arXiv:1104.5100.

Recepción: 02/05/2018. Aprobación: 06/08/2018.

Resumen

Esta reflexión es un ejercicio epistemológico que intenta describir el proceso de objetivación de las matemáticas como uno de los muchos modos humanos de objetivar, conocer y construir mundo. Es también una invitación a no cerrar nuestra capacidad cognitiva y a mantenerla abierta a nuevas objetivaciones posibles y construcciones de realidad.
Palabras clave: objetivar, conocer, realidad, matemáticas, números, cantidad.

The reality of mathematical entities

Abstract

This reflection is an epistemological exercise that attempts to describe the process of objectifying mathematics as one of the many human ways of objectifying, knowing and constructing the world. It is also an invitation not to close our cognitive ability and to keep it open to new possible objectifications and constructions of reality.
Keywords: Objectifying, knowing, reality, mathematics, numbers, quantity.

Introducción

El “objeto” de las ciencias no existe como tal, lo que existe para el ser humano es el bombardeo sensorial continuo y dinámico de una realidad1 confusa, maleable, que se nos impone y nos atrapa inevitablemente, pero que también nos seduce, eclosiona a nuestro alrededor y en nosotros mismos, que nos hunde y nos eleva, que nos arrebata y nos estruja, que nos maravilla y desespera.

“Realidad” es una palabra de origen latino cuya traducción al español bien podría ser “coseidad” (la expresión de “cosa” en abstracto), pero una coseidad en la que todo es uno y en la que estamos inmersos hasta la médula, muy a pesar de nuestra inteligencia racionalizante y de su tendencia permanente a objetivar, es decir, a poner distancia, a poner frente a “uno” lo “otro”, como si “uno” no fuera lo “otro” y como si lo “otro” no estuviera de alguna manera en “uno”. Dicho en otras palabras, como si en verdad hubiera algo “otro” y algo “uno” separados.

Cuando no es así, uno mismo es un flujo constante e interminable –mientras vivimos– de pensamientos, sensaciones, sentimientos, sueños y fantasías. Uno mismo sólo se puede denominar “uno” y “yo” con el esfuerzo enorme de retenerse y compactarse en la memoria y objetivarse en la autoconciencia. Esfuerzo en el que se juega nuestra misma racionalidad y lucidez; debido a lo cual, en sus altares quemamos las fantasías “disparatadas”, las locuras no funcionales (o tal vez funcionales, pero en mundos alternos), lo sueños del inconsciente y las preguntas de los niños. Y también limitamos con leyes y costumbres a nuestra libertad, siempre peligrosa y vista bajo la lupa de la sospecha (por ser nuestra apertura a lo posible y, por lo mismo, a lo nuevo).

Este universo del que somos parte, especialmente el universo humano, nos modula y en él nos moldeamos juntos, desde pequeños, a tal grado que –con el paso de los años– olvidamos nuestros sentires primarios y reducimos nuestro sentir a lo ya sentido, lo encajonamos en las reminiscencias de lo ya vivido y aprendido; percibimos lo que nos enseñaron a percibir, y actuamos como nos enseñaron a actuar y, o nos volvemos parte del grupo que sanciona, o seremos sancionados, lo cual puede significar –en muchos casos– la expulsión, la segregación, las etiquetas descalificadoras, el ostracismo. Uno se puede convertir en el extraño al que se tiene que tolerar o el chivo expiatorio al que se debe condenar.

Lo interesante de todo esto es que el que no se asombra con una sensibilidad abierta, el que no pregunta lo que no entiende o no sabe –a pesar de lo obvia que pueda parecer la pregunta–, el que no se lanza a la aventura de la libertad, no sólo se cierra y se va endureciendo, sino que también hace lo mismo con esa realidad con la que se es uno y de la que se está falsamente escindido. También encerramos de manera determinista a lo “otro” y a los “otros”: a todo lo que nos rodea, a nuestra familia, a nuestra sociedad, a nuestro mundo, al universo entero. Afortunadamente, la dinamicidad de la realidad misma no permite que la fosilización sea completa, siempre hay explosiones, resistencias y mutaciones, y siempre necesitaremos viejas preguntas para lo nuevo y nuevas respuestas para lo viejo y, por lo mismo, nuevos tanteos de la libertad liberada de trabas y caminos ya hechos, nuevas caídas y nuevos comienzos.

Así, precisamente así, es como nace y sigue naciendo la ciencia, porque podemos separarnos de la realidad de la que somos parte y podemos dividir a su vez esa misma realidad en millares, millones de “objetos”. Los que a su vez fragmentamos cada vez más para una mejor comprensión y luego nos volvemos locos por volver a unir, porque el costo de la profundización en segmentos cada vez más fraccionados de la realidad, es, en última instancia, el de perder de vista la totalidad y, parafraseando a Salvador de Madariaga (Yuste y Rivas-Caballero, 2016, tercera parte), el peligro de saber cada vez más, acerca de menos. Así que ahora volteamos a nuestro alrededor en busca de otros supuestos “yoes”, que con su mucha profundización en su “objeto propio” nos ayuden a recomponer el rompecabezas en que hemos convertido a la realidad, para, entre todos, recuperar un poco de la unidad perdida en la torre de Babel en que se ha convertido la especialización, y comprender mejor, desde un panorama más amplio que el de la propia mirada fija en un solo punto.

De alguna manera, se trata de un proceso dialéctico, en el que el en sí de la especialidad propia, tiene que confrontarse al fuera de sí de otras especialidades para desalinearlos todos –los en síes y los para síes, los “objetos” y los “sujetos”–, y alcanzar una cierta síntesis en la que lo que se pierdan sean las fronteras, antes infranqueables, de los “objetos” y los egos del especialista; y lo que se gane sea el conocimiento dialógico especializado, pero no cerrado a lo diferente, sino abierto y en reunificación continua.

Detengámonos a reflexionar por un momento en esos primeros procesos de distanciamiento que han dado origen a nuestras ciencias y a los modos que tenemos de comprenderlas y, por lo tanto, de vivirlas; porque volver sobre nuestros pasos hacia atrás puede ayudarnos a desmitificar lo que, sin mucho cuestionamiento, damos por hecho respecto a ellas.

Esta reflexión se centrará entonces en la “reina de las ciencias”, ni más ni menos que en las muy antiguas y respetables matemáticas. Tan respetables, que muchas otras ciencias se apresuran a ponerse en los primeros lugares muy cerca de ellas, tan sólo porque se expresan en su lenguaje. Y otro montón de ciencias de las denominadas sociales y de las humanidades, han hecho esfuerzos valerosos por asumirse como científicas tan sólo porque intentan, o utilizan un lenguaje matemático y métodos cuantitativos para su análisis de datos.

El objeto de las matemáticas

Desde luego que los números no se encuentran dentro de la calculadora, ese aparato no podría tener números si nosotros no lo hubiéramos determinado así. De hecho, aún la numeración que usamos es una construcción y una elección. Los antiguos griegos formaban sus números con puntos, los romanos con letras; pero fueron los números arábigos (cuya función posicional parece que los árabes tomaron de los indios, junto con el uso del cero) los que resultaron más prácticos para, con una nomenclatura sencilla, trabajar y calcular todo lo que se puede “decir” numéricamente hablando: del 0 al 9 tenemos todo lo que necesitamos para expresar cualquier cantidad.

Y he ahí la cuestión, los números son un lenguaje para expresarnos, por eso tantas ciencias pueden recurrir a ellos y tantas otras lo intentan (aunque las particularidades más específicas de los objetos de estudio de ciertas ciencias no sean precisamente expresables en términos matemáticos). Pero los números no son el objeto de las matemáticas, el objeto de las matemáticas es una abstracción, en ella abstraemos por ejemplo la cantidad: lo cuanto.2

¡Qué maravilla! Tenemos la capacidad de abstraer de la realidad la cantidad y solamente la cantidad. Los matemáticos de profesión son una especie de cernidor, que anda por ahí separando las pepitas de oro del lodazal. Para ellos las pepitas de oro son todo lo cuanto, lo cuantificable del universo, y el lodazal que queda es nada más y nada menos que el resto de lo real.

Y la metáfora no es tan equívoca como pareciera, en un lodazal todo parece indiscernible, y sin embargo los gambusinos lograron sustraer oro, y los biólogos seguro encontrarán otras cosas, y los químicos otras, y los niños jugando a las “cocinitas” ¡ni se diga! Todos tenemos la capacidad de objetivar, de distanciarnos, de apreciar sólo uno o unos pocos aspectos del lodazal de lo real, para seguir con la misma metáfora.

Ahora, entremos a la cabeza del matemático: la cantidad no huele, no se ve (su expresión sí, ya lo hemos dicho, pero la expresión no es la cantidad, sino su vehículo), no tiene textura, ni temperatura, no sabe a nada, no hace ruido; en otras palabras, es en extremo abstracta, casi inasible. Por eso, en buena medida, la dificultad que nos presentan las matemáticas a la mayoría de los mortales más acostumbrados a andar por la vida olfateando el viento, escuchando una canción o imaginando animales en las nubes.

La cantidad sólo puede tener medida, y si involucramos a la cantidad en el espacio, entonces, la cantidad se configura y tenemos la geometría. Pero la cantidad es un juguete muy divertido, se puede sumar, restar, multiplicar, dividir, “quebrar”, calcular, y un largo etcétera ad infinitum, porque las ciencias exactas también trabajan con el infinito. Desde la ausencia de cantidad, denominada con aquella expresión con la que solemos comparar a muchos burócratas: “un cero a la izquierda”; hasta la cantidad con la que muchos han equiparado al no cuanto por excelencia: Dios, el Infinito, el Aleph.

La cantidad también se puede exprimir y así expresar lo aparentemente inexistente en el lodazal de lo real, como los números negativos. O puede ser irracional y llevarnos a números que, por facilidad, en algunos casos, expresamos con letras griegas como π ο φ, ya que, por contener infinitos decimales, nunca acabaremos de expresarlos en notación arábiga. Y la cantidad en el espacio nos lleva a figuras maravillosas, perfectas, tan perfectas que no tienen parangón con lo real que conocemos en la cotidianidad, aunque eso real se les parezca un poco: el círculo, el triángulo o el icosaedro, por eso “debemos ser cuidadosos en distinguir las entidades matemáticas precisas de las aproximaciones que vemos a nuestro alrededor en el mundo de los objetos físicos” (Penrose, 2014, p. 53).

Pero… ¿no hemos abstraído la cantidad de lo real cotidiano, de esos objetos físicos a los que ahora debemos aplicar lo abstraído con cuidado? Pareciera que en eso que hemos denominado “realidad” sólo hay dos clases de “cuantos cuantificables” –valga la redundancia– los continuos y los discretos. Los continuos –como el tiempo y el espacio– son indiscernibles en lo que a medida se refiere, y, por eso, nosotros los fragmentamos y medimos arbitrariamente y con medidas externas que nos inventamos. Por ejemplo, al tiempo lo segmentamos en fracciones y hablamos de 1 hora y 46 minutos, o al espacio lo medimos para construir algo y especificamos que lo requerimos de 2 metros y 3.52 centímetros.

En cambio, los cuantos discretos son en general unidades agrupadas que se pueden fragmentar, pero cuya cantidad y peso están ahí en ellas, aunque nosotros nos inventemos los números para expresarlas como cuando decimos el peso de un cuerpo sólido en kilogramos.

Pero, entonces, vuelvo a mi pregunta, pero la reformulo: si las matemáticas son una abstracción que nosotros hemos hecho de lo cuanto (en este artículo nos centramos en lo cuantitativo de las matemáticas), de la cantidad de aquellas cosas a las que denominamos “reales” como, por ejemplo, las vacas, los árboles, las construcciones arquitectónicas y el agua, ¿por qué terminan las matemáticas trabajando con figuras perfectas, con cantidades infinitas, con números negativos y con otras muchas cosas que no encontramos como tal en la realidad cotidiana? Y agrego una pregunta más, ¿por qué las ciencias exactas resultan ser tan sólo probables y aproximativas al medir la cantidad de lo “real” (nuestro mundo cotidiano: las vacas, los árboles, el agua, los puentes, los grupos sociales)? ¿No hay algo aquí que no cuadra?

Y aprovechando que ya estamos metidos en el filosofar, vayamos más lejos aún, ¿no son reales también los números, las figuras perfectas y los números irracionales aun cuando no los percibimos igual que a las aves y las estrellas? ¡Desde luego que sí! Porque, volviendo al inicio de nuestra reflexión, nosotros no somos un “uno” separado de lo “otro”, lo que denominamos “otro” está también en nosotros y tiene muchas maneras de habitarnos, al igual que nosotros en nuestra supuesta “unicidad” habitamos todos los mundos posibles, todos los “objetos” que recortamos y abstraemos de aquella supuesta realidad “otra”. Y como nos habitan y los habitamos, estos objetos abstraídos son realidad, no sólo en nuestras cabezas, sino también en todo lo que nos rodea. La cuestión es que se pueden hacer muchos matices en eso que denominamos “realidad”, las ideas abstractas son también realidades y cuando las utilizamos para comprender y transformar lo natural cotidiano, como una piedra o un trozo de madera, la realidad de lo abstracto termina imponiéndose a la realidad de lo cotidiano de donde fue abstraída. Se impone porque se vuelve una herramienta para transformar esa realidad cotidiana y construir nuevas realidades.

Es así como al detectar una nueva perspectiva de lo real y al abordarla abstrayéndola, esta nueva abstracción nos hace y la hacemos pensar, nos hace y la hacemos hablar, nos hace y la hacemos resonar. Y esa resonancia no es otra cosa que el cultivo lento y paulatino que vamos haciendo con esas semillas “objetuales” –semillas de lo que será “objeto” de estudio, lo que “objetivaremos”–, regadas y abonadas con la sensibilidad y la inteligencia humanas; y eso, cultivado de tantas maneras distintas y a través de las épocas, es lo que denominamos cultura: “el conjunto aprendido de tradiciones y estilos de vida socialmente adquiridos, de los miembros de una sociedad. Incluyendo sus modos pautados y repetitivos de pensar” (Harris, 2011, p.20). Los seres humanos nos cultivamos, nos culturizamos al construir un mundo en común, y construimos este mundo al compartirnos los unos con los otros todo aquello que vamos seccionando de lo que nos rodea para convertirlo en “objeto”, ya sea de estudio, de gozo, de consumo, de uso, o de un largo etcétera.

En este sentido, los números son ontológicamente reales; es decir que existen con la misma fuerza de imposición –o tal vez más– que un árbol y forman parte del mundo humano que compartimos. Así, también son reales las figuras geométricas, los axiomas, las fórmulas y los teoremas. Por eso podemos hacer taxonomía de los números y clasificarlos con hermosos diagramas, y hacer ábacos, calculadoras y computadoras; por eso podemos contar, medir, pesar, calcular y sufrir o gozar con las matemáticas; porque sus frutos son reales y tangibles y sus aplicaciones, también. Y así como objetivamos con las matemáticas, también lo hacemos con la química y con la biología, y con las sociedades y con las conductas; y cultivamos y damos frutos. Lo mismo sucede con el arte, con los juegos de los niños y con la comida de la cocinera: sacamos la semilla que es el “objetivar”, seccionando algo de lo que denominamos “real” dentro de nuestra cotidianidad, y lo regresamos después, pero transformado a esa misma realidad de donde lo sacamos. Con eso enriquecemos nuestro entorno y nos enriquecemos y nos ensanchamos nosotros mismos como realidad.

El problema aquí, me parece que no es esa maravilla de las ciencias, las artes y la cultura en general. El problema es que, al objetivar (abstraer, fragmentar de un todo mayor), al ser convertido en notación, en lenguaje, en producto, en un algo aparte de aquello de donde se separó, lo objetivado (ya no se trata de la cantidad de un elefante, ni de la figura de una columna), la cantidad abstracta misma, pasa a formar parte de nuestro entorno como una cosa, como un objeto más de nuestra realidad humana: como número, como medida, como figura geométrica, por ejemplo.

El problema está, entonces, en el olvido de sus orígenes, el olvidar que mucho de lo que nos rodea y de lo que somos no es así a fortiori, sino que así lo hemos hecho nosotros y, por lo mismo, es también cuestionable y transformable. Al olvidar los orígenes del conocimiento que vamos construyendo, en lugar de ampliar, reducimos nuestras posibilidades de crecimiento. En el caso de las matemáticas, “La pregunta ‘La matemática ¿es descubierta o inventada?’ no está bien formulada, porque implica que la respuesta debe ser una o la otra y que ambas posibilidades se excluyen mutuamente” (Livio, Mario, 2011, p. 235), cuando realmente, la respuesta es ambas posibilidades: descubrimos la cantidad, la abstraemos, la procesamos, la pensamos, la reinventamos, la expresamos, y luego aplicamos todo esto que hemos hecho e inventado, con la visibilizada y objetivada cantidad, a todo lo cuanto que nos rodea.

Olvidar la parte creativa de todo esto y dar las cosas por supuestas hace que no se nos ocurra la posibilidad de cuestionarlas, revisarlas y de intentar abrir nuevos caminos, “así, por cierto, puede una racionalidad unilateral, llegar a ser un mal” (Husserl, 1998, p. 113). Somos parte activa de esa realidad fluctuante que nos hace y constituye, pero a la que también nosotros hacemos y constituimos, y prácticamente todo lo que conocemos, lo conocemos ya pensado, digerido y reinventado por los otros que han intervenido activamente en la construcción de mundo.

Si no somos conscientes de nuestra capacidad de objetivar y con esto de actuar para transformar y transformarnos, ni de detectar que las objetivaciones que hacen, en este caso las ciencias, no son cosas en sí ni inamovibles, seremos solamente una parte pasiva de esa fluctuación y, al ser pasivos, seremos también zarandeados, abrumados, y objetivados, digeridos y reinventados por quienes sí trabajan activamente en la constitución del mundo (con independencia de los intereses que los muevan a esto). Así que, ¡busquemos la cuadratura del círculo! Tal vez con otras objetivaciones del espacio esto pierda el carácter de imposibilidad que, de momento, aparenta tener.

Pero, al hacer esto, no debemos olvidar que las objetivaciones ya hechas por la ciencia llevan consigo toda una carga de supuestos: las primeras miradas con las que se han objetivado sus problemas tienden a comprenderse como las únicas maneras posibles de mirar. Las construcciones metodológicas, en muchos casos de exquisita precisión, dependen de esas miradas que se dan por supuestas y ayudan a ver sólo lo que esas miradas nos permiten ver. Los modos de experimentación, de ser el caso, responden también a lo que esas miradas ya supuestas alcanzan a vislumbrar. Los rituales y modelos para informar son fruto de esas visiones oficialmente sancionadas. Por lo mismo, si queremos encontrar la cuadratura del círculo, tendremos tal vez que dejar de mirar por un tiempo, tal vez sea el momento de tantear para aprender a mirar con nuevos ojos, en lugar de sólo mirar para luego tocar solamente lo ya visto.

Imposible objetivar de otro modo las cosas mientras sigamos en el horizonte de las miradas heredadas por siglos de hacer ciencia sólo bajo ciertas perspectivas. ¡Cerremos los ojos! ¡Olfateemos nuestro objeto de estudio! ¡Escuchémoslo también!

Aprendamos a saborearlo con la inteligencia atenta, más que a la respuesta, a la posibilidad de nuevas preguntas. Esto, desde luego, resulta heterodoxo pues es herético dentro de los modos convencionales de hacer ciencia. Pero no existía la ortodoxia, ni la ciencia, antes de las primeras objetivaciones. La ortodoxia se fue construyendo sobre la marcha, y no lo hizo de una manera lineal y sin disrupciones; ni mucho menos, de un modo neutral, como lo percibimos a la distancia dentro de las ciencias ya constituidas.

No se trata de la herejía per se, sino del riesgo que hay que asumir si pretendemos crecer en realidad y en conocimiento, lo que, en última instancia, para el Homo sapiens, viene a ser exactamente lo mismo.

Referencias

• Aristóteles. (2014). Metafísica. Madrid: Gredos.
• Castoriadis, C. (2004). Sujeto y verdad en el mundo histórico-social. México: FCE.
• De Souza santos, B. (2009). Una epistemología del sur. México: FCE.
• García, R. (2000). El conocimiento en construcción. De las formulaciones de Jean Piaget a la teoría de sistemas complejos. Barcelona: Gedisa.
• Harris, M. (2011). Antropología cultural. Madrid: Alianza Editorial.
• Heidegger, M. (2016). Ser y Tiempo. Madrid: Editorial Trotta.
• Husserl, E. (1998). Invitación a la fenomenología. Barcelona: Edición Paidós I.C.E./U.A.B.
• Husserl, E. (2016). Renovación del hombre y la cultura. Cinco ensayos. Barcelona: Anthropos.
• Kuhn, T. (2004). La estructura de las revoluciones científicas. México: FCE. Livio, M. (2011). ¿Es Dios un matemático? Barcelona: Ariel.
• Penrose, R. (2014). El camino a la realidad. Barcelona: Debate.
• Rábade, S. (2010). Teoría del conocimiento. Madrid: Akal.
• Yuste, B. y Rivas-Caballero, S. L. (2016). María Sklodowska Curie. Ella misma. Madrid: Ediciones Palabra.

Recepción: 6/3/2017. Aprobación: 9/8/18.

Resumen

La acidosis tubular renal (ATR) distal es una enfermedad que provoca retraso en el crecimiento óseo, depósitos de calcio en el riñón, debilidad muscular y sordera. La ATR es una de las más de siete mil enfermedades raras conocidas en el mundo. Objetivo. Evaluar el impacto de los sitios www.funatim.org.mx y www.acidosistubular.unam.mx, su página de Facebook y un canal de Youtube, para contactar pacientes con el diagnóstico de ATR. Métodos. El análisis estadístico comprendió el diseño de la medición, la recolección de los datos y el análisis de la información. Resultados. Los medios digitales atrajeron a 3 pacientes con ATR y a cientos de familias con falsos diagnósticos. Predominó la participación de mujeres de la Ciudad de México y Jalisco; se tuvo alcance en 113 países. Algunas publicaciones en Facebook llegaron a más de 20,000 usuarios y a más de 70,000 en el sitio web durante un lapso de 4 años. Conclusiones. Las redes sociales conformaron una comunidad sólida que alertó los falsos diagnósticos y, a través de change.org, lograron que la Secretaría de Salud publicara la “Guía de práctica clínica para el diagnóstico y tratamiento de la acidosis tubular renal en pacientes pediátricos”.

Digital spaces and rare diseases

Abstract

Introduction. Distal renal tubular acidosis (RTA) is a rare disease that provokes failure to thrive, calcium deposits in the kidney, muscular weakness and deafness. RTA is one of the more of seven thousand of rare diseases known around the world. Objective. Evaluate the web sites www.funatim.org.mx and www.acidosistubular.unam.mx, a Facebook page of followers and a YouTube channel, to contact patients with the diagnosis of RTA. Methods. The statistical analysis comprised the design of measurements, data collection and analysis. Results: Digital media attracted 3 patients with RTA and hundreds of families with false diagnosis. Most participants were women from Mexico City and Jalisco; digital publications was consulted by 113 countries. Some Facebook postings reached more than 20,000 users and more than 70,000 through the website during a period of 4 years. Conclusions: Social networks conformed a solid community to alert misdiagnosis. Through a request in change.org to the Ministry of Health, they achieved the publication: “Guide of clinical practices for the diagnosis and treatment of Renal Tubular Acidosis in pediatric patients”.

Introducción

Aproximadamente 7% de la población mundial padece de alguna enfermedad rara, lo que equivale a cerca de 500 millones de personas. La legislación europea establece un límite de prevalencia menor de 5 casos por cada 10 mil personas para definir la rareza (FEDER, 2009). La Federación Mexicana de Enfermedades Raras (Femexer) estima que en México 7 millones de personas sufren de una de las 7 mil enfermedades raras existentes reconocidas por la Organización Mundial de la Salud (OMS). El problema al que se enfrentan las familias con una enfermedad rara en países en desarrollo, es la falta de información confiable y accesible y de centros especializados donde atenderse; esto retrasa su diagnóstico y, por lo mismo, su tratamiento. En contraste, algunos países desarrollados tienen centros especializados y asociaciones dedicadas a pacientes con enfermedades raras y llevan a cabo investigación clínica y traslacional. La investigación traslacional consiste en llevar las preguntas que surgen en los hospitales a un laboratorio de investigación y, a la inversa, los hallazgos que se encuentran en el laboratorio, trasladarlos a la clínica para mejorar el tratamiento de los pacientes.

A pesar de los avances en la comprensión de varias enfermedades raras, la patogénesis (es decir, el origen y desarrollo) de muchas otras ha permanecido en el desconocimiento debido a que la mayoría de las enfermedades raras son complejas y tienen un origen genético; por otra parte, pocos médicos las conocen.

Respecto a las enfermedades renales, existen varias que son hereditarias en por lo menos 10% de los pacientes con insuficiencia (Soliman et al, 2012); también hay factores genéticos que influyen en la progresión del daño crónico en las enfermedades renales adquiridas (Devuyst et al, 2014). Las enfermedades renales hereditarias tienen frecuencias variables; por ejemplo, la enfermedad poliquística del riñón autosómica dominante es la más frecuente y afecta a 1:1000 personas. En contraste, el resto de las enfermedades renales hereditarias son raras.

La dieta proteica occidental produce aproximadamente 1 miliequivalente (mEq) de hidrogeniones (H+) por kg de peso corporal al día. En ausencia de un amortiguador en el plasma, la producción diaria de H+ disminuiría el pH sistémico de 7.4 a 3 en tan sólo una hora, lo cual es incompatible con la vida. Por ello, el par ácido/base: CO2/ bicarbonato (HCO3-), constituye el amortiguador más importante porque mantiene el pH constante en el ambiente intra y extracelular.

El riñón filtra al día cerca de 180 litros de sangre y evita que perdamos el bicarbonato. El riñón expulsa la carga ácida proveniente de nuestra dieta proteica en forma de amonio; el ión amonio (NH4+) es un ácido que se disocia en agua en amoniaco (NH3). El par NH4+/ NH3 hace que el pH de la orina tenga valores entre 5 y 6, lo cual permite que se deseche la carga ácida sin causarnos problemas.

La acidosis tubular renal (ATR) distal es una enfermedad en la que los pacientes no pueden eliminar el amonio en la orina, por lo que éste consume el bicarbonato de la sangre y se desarrolla acidosis metabólica con cloruro mayor al normal: pH menor de 7.4, niveles de bicarbonato menores de 16 mM; se forman depósitos de calcio en el riñón, disminuye el potasio en el plasma, lo que puede provocar parálisis muscular y arritmias. La respiración también se acelera y se desarrolla sordera nerviosa temprana o tardía (Escobar et al, 2013). La ATR tiene una prevalencia menor de 1 en un millón en la población en general y de 1 en 10 mil en sociedades con matrimonios consanguíneos (Elhayek et al, 2013). En el Reino Unido se documentó el primer estudio genético de ATR distal con 75 pacientes, la mayoría de origen turco (Stover et al, 2002); en España se han documentado 6 niños hispanos (Gil-Peña et al, 2014) y 8 casos de otros países (Gómez et al, 2016).

El grupo de investigación de la Dra. Laura Escobar descubrió una proteína en el riñón que transporta amonio (Carrisoza-Gaytan et al 2011). Fue entonces que se preguntaron: ¿qué pasa si esta proteína no funciona? Pues se acumularía amonio y, entonces, éste reaccionaría con el bicarbonato de la sangre, y eso es justo lo que sucede en los pacientes que tienen ATR distal. Así, la Dra. Escobar inició la búsqueda de pacientes con este padecimiento renal con el objeto de analizar sus genes. Pronto se percató que no existían casos documentados de ATR en la población mexicana. Para contactar familias con ATR publicó el blog blog www.funatim.org.mx (2010) y luego www.acidosistubular.unam.mx (2013), contactamos a cientos de familias con el diagnóstico de ATR.

El objetivo del trabajo fue evaluar el impacto que ha tenido la presencia digital de la Fundación para la Acidosis Tubular Renal Infantil Mexicana, A.C. (FUNATIM), en la difusión de información sobre ATR y diversos temas de salud; además de orientar a las familias que han sido erróneamente diagnosticadas con este síndrome en nuestro país.

Materiales y métodos

Para el análisis estadístico se desarrolló un marco conceptual de cuatro etapas: 1) diseño de la medición (revisión de métricas y dimensiones relacionadas con la visibilidad en medios digitales), 2) recolección de los datos (identificación de herramientas de analítica digital, desarrollo y aplicación de filtros de búsqueda), 3) análisis de la información (desarrollo de un análisis cuantitativo y cualitativo, orientado a destacar el impacto de los canales digitales) y 4) presentación de resultados (selección de gráficos representativos del análisis de acuerdo a las características de cada canal digital).

Se utilizaron como instrumentos: Google Trends (análisis orgánico), Google Analytics (analítica web), módulo nativo de estadísticas de Facebook y FanpageKarma (página de fans de Facebook) y el módulo nativo de Youtube Analytics (canal de Youtube). Para el análisis orgánico se revisó el periodo de 2004 a 2017, mientras que para el sitio web se analizaron los datos recopilados a partir del 31 de enero del 2013, fecha en que se comenzó a obtener estadística del sitio www.acidosistubular.unam.mx. Para la página de Facebook se analizó la información a partir del 30 de abril del 2013 y del canal Youtube a partir del 27 de abril del 2015. Para fines del presente trabajo se analizó la información hasta el 27 de enero del 2018.

Análisis de tendencias de búsqueda

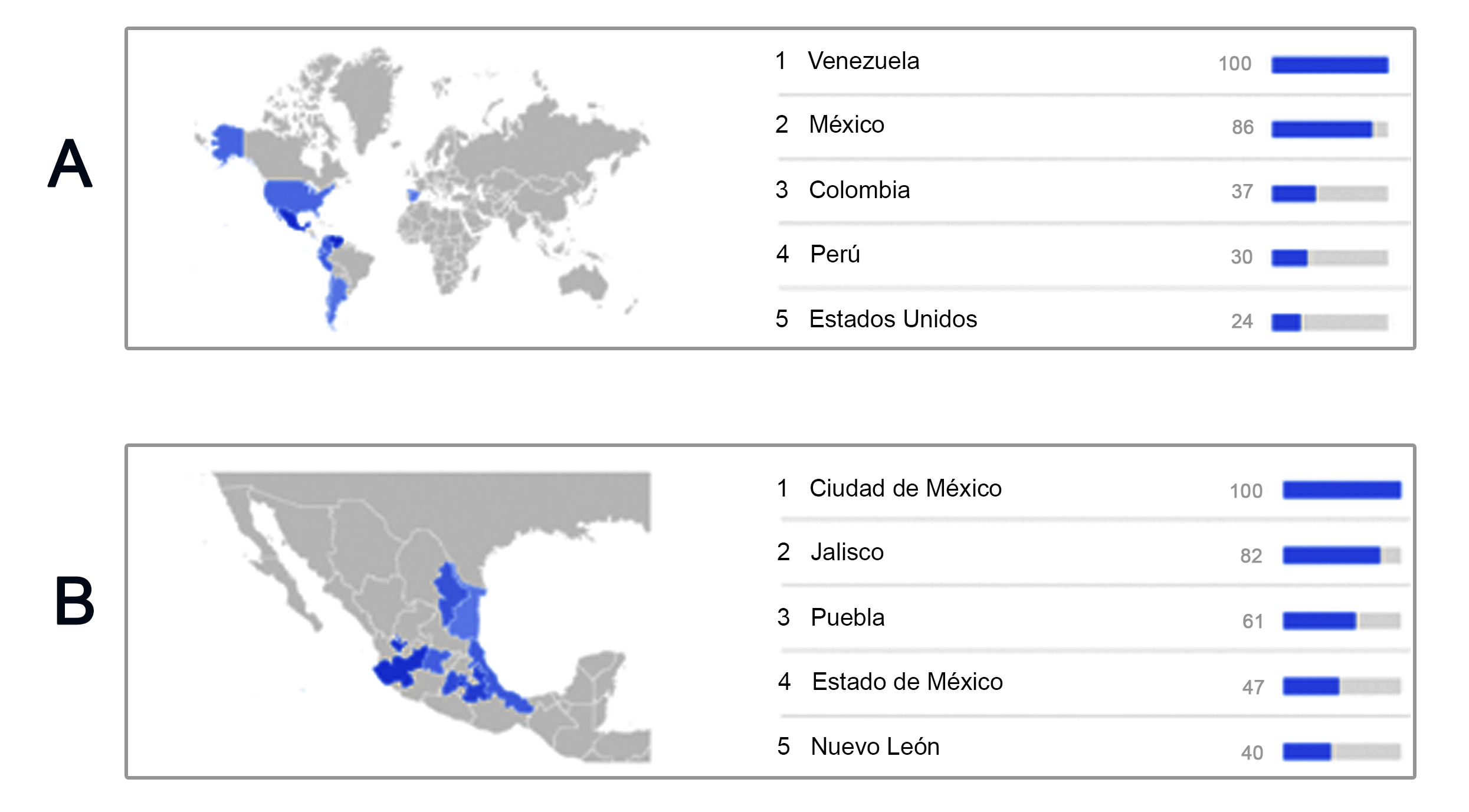
Para evaluar el impacto de la presencia digital, se analizó la tendencia del término “acidosis tubular renal” a través del tiempo, desde el motor de búsqueda Google. Se encontró que, a nivel internacional, el término ha sido buscado con mayor frecuencia por usuarios de Venezuela, México y Colombia (fig. 1a). A nivel nacional, las regiones de interés en donde se han realizado las consultas del término han sido: Ciudad de México, Jalisco, Puebla, Estado de México y Nuevo León (ver figura 1b).

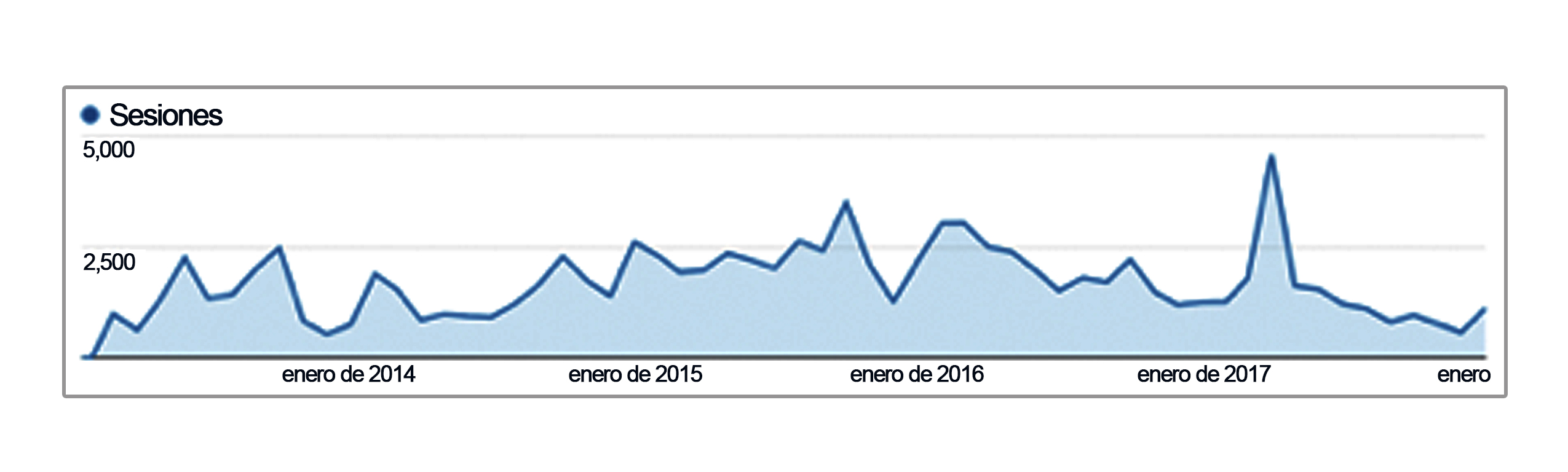
En el análisis de tendencia para el término “acidosis tubular renal”, se observó que antes del 2005, las búsquedas del término eran más frecuentes; posterior a este periodo la tendencia disminuyó; sin embargo, para abril del 2011 y mayo del 2012 se presenta un nuevo interés en la búsqueda de dicho término, con la variante de: “acidosis tubular renal en niños” (ver figura 2).

Sitios web de la FUNATIM

El primer canal de difusión de la Fundación fue el sitio web www.funatim.org.mx. Para el periodo en el que permaneció activo (2010-2013), el principal objetivo era poner a disposición del público interesado un canal informativo. La mayoría del contenido presentado eran textos y la comunicación con el público era a través de correo electrónico o de manera presencial.

Además de la puesta en línea del sitio web, se publicaron 2 artículos (Muñoz et al 2012; Escobar et al 2013) y 5 notas en medios externos (SIPSE, el blog de Acidosis Tubular Renal, Monografías, en el Boletín DGCS-UNAM y Mamá freelance). Con el objeto de analizar su impacto, se observó la cantidad de veces que los enlaces asociados a los artículos, notas y enlace del sitio actual, fueron compartidos. Además del sitio web (1,110 veces compartido) las notas: “Alertan de fraude con rara enfermedad”, “Boletín UNAM-DGCS-514”, y “Enfermedades de moda y su sobre diagnóstico” fueron las más compartidas en Facebook.

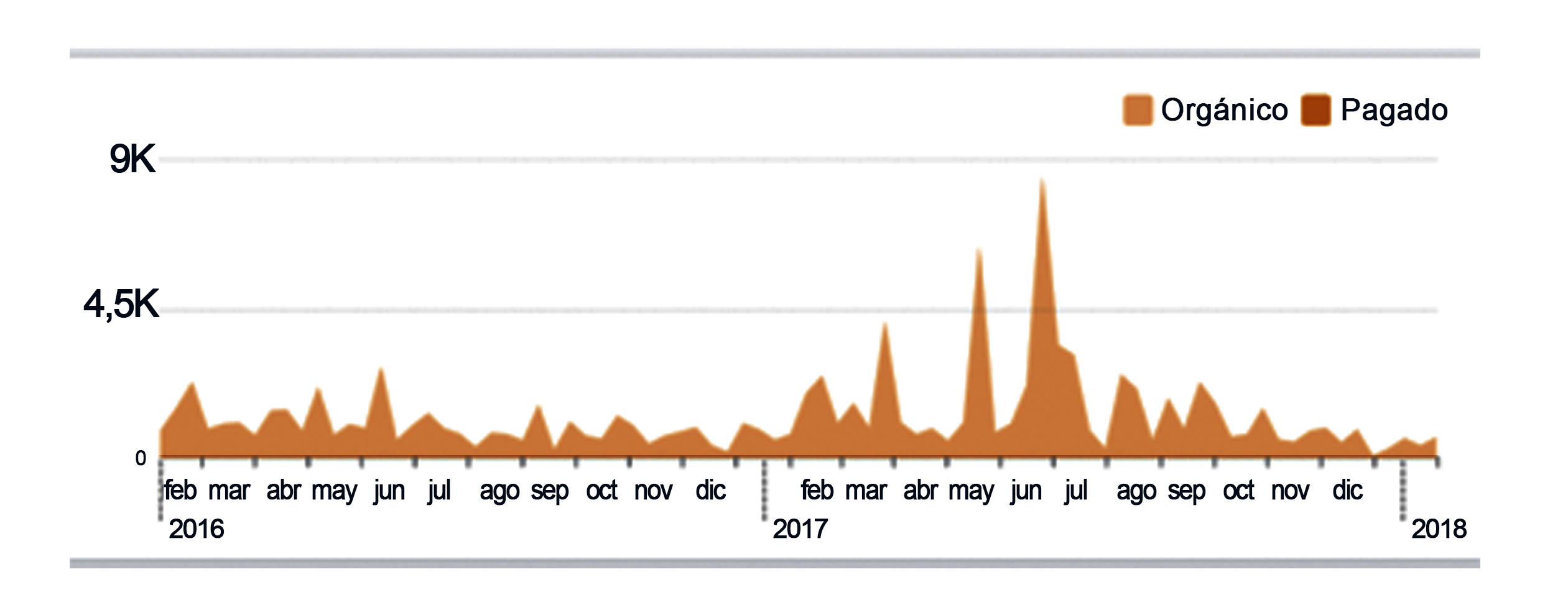
Con la evolución de la comunicación en medios digitales, y la necesidad de compartir contenidos multimedia, fue necesario actualizar la estructura del sitio de la FUNATIM. Por tal motivo, el 21 de diciembre del 2012 se publicó una nueva versión alojada en el dominio institucional de la Universidad Nacional Autónoma de México (UNAM), en la dirección electrónica: www.acidosistubular.unam.mx. Cabe señalar que hasta marzo del 2013 se agregó un código de seguimiento para recolectar información estadística sobre la adquisición y comportamiento del sitio web, mediante el uso de Google Analytics. En el periodo comprendido entre el 4 de marzo de 2013 y el 27 de enero de 2018, se recibieron un total de 101,397 visitas, un promedio de 1,600 visitas mensuales (fig. 3). Durante marzo de 2017, el sitio alcanzó cerca de 4,589 visitas y entre junio-julio cerca de 9 mil. El sitio ha sido consultado en 115 países de los cuales 78% de las visitas proviene de México.

En la tabla se muestran los 10 países y las 10 ciudades de donde provienen la mayor cantidad de visitas. La Ciudad de México, el Estado de México y Jalisco son las que presentan mayor actividad.

En cifras del sitio web se encontró que 73% de los visitantes que lo consultan son mujeres mientras que 27% son hombres, en su mayoría entre los 25 y 34 años. Éste se ha convertido en un espacio de contenidos relacionados con la ATR, que está indexado y posicionado en buscadores en México. Los contenidos más consultados por los visitantes son: “¿Qué es el ATR?” (con 49,051 visitas; 31.73%) y “¿A quién consultar?” (con 12,170 visitas; 7.87%).

Principales países y ciudades de donde provienen las visitas al sitio web de FUNATIM (periodo 31 enero 2013 – 31 julio 2017). Fuente: Google Analytics.

Principales fuentes de tráfico

La mayoría de los usuarios que llegan al sitio web lo hace a partir de búsquedas en Google, esto se debe al buen posicionamiento del dominio unam.mx al que se encuentra asociado el sitio de la FUNATIM. Del total, 56.54% llega al sitio web a partir de búsquedas en Google organic search, seguido por los usuarios que ingresan directamente colocando la dirección electrónica del sitio en el navegador Direct (18.90%), la tercera fuente y la más importante de esta investigación, pues se refiere a los visitantes que llegaron al sitio de la FUNATIM a partir de alguna red social (12.72%) y finalmente referral (11.82%) que se refiere a las visitas al sitio a través de un vínculo o referencia en sitios web externos (sitios de noticias, blogs, portal UNAM, entre otros).

Las redes sociales como fuente de adquisición

Al realizar el análisis de las redes sociales que actúan como medio de adquisición al sitio web de la FUNATIM, se encontró que de las 12,915 sesiones que vienen de Social, 93,16% provienen de Facebook donde la URL más compartida ha sido la página de inicio del sitio web.

Página de seguidores (fans) de Facebook

La página de fans de Facebook ha sido un canal de vinculación importante para la FUNATIM, pues fue a través de este canal que en agosto del 2013 cerca de 1,200 familias solicitaron, en el sitio Change.org a la Secretaría de Salud Pública (SSP) elaborar una guía de diagnóstico de ATR. En un hecho insólito, en enero del 2017 la SSP publicó la “Guía de prácticas clínicas para el diagnóstico y tratamiento de la ATR en pacientes pediátricos”.

La página de fans Acidosis Tubular Renal-SIPSE creada en abril del 2013 tuvo, hasta enero de 2018, 2 551 Me gusta. Acorde a la comunidad digital, la página de fans también se conforma en su mayoría por mujeres (80%), principalmente entre los 25 y 34 años, provenientes de México (Ciudad de México y Guadalajara); dato que coincide con las búsquedas orgánicas y el análisis geográfico del sitio. En promedio se realizan 3 publicaciones diarias, con un nivel de servicio de 86%; es decir, que en menos de 14 horas se brinda una respuesta a las preguntas de los usuarios. La labor de publicación se ha realizado todos los días de la semana, abarcando en promedio un horario de las 8:00 a las 23:30 horas. Los días de mayor interacción son los lunes por la noche y los jueves por la mañana.

Con la finalidad de mantener informada a la comunidad, se comparten notas, contenidos y consejos relacionados con la ATR, nutrición infantil y temas de salud en general.

La gestión de la página de fans se ha basado en la estrategia de contenidos especializada en el tema central: ATR, y sin el uso de anuncios pagados. De esta forma, se ha conseguido el crecimiento paulatino de manera orgánica (ver figura 3).

Entre las publicaciones que destacan por la respuesta positiva de la comunidad se encuentran las siguientes:

1. “Estudio de investigación clínica que se realizó en el Hospital Centro Médico IMSS la Raza”, con un alcance de 20,557 personas (https://bit.ly/2MaQafz).
2. “Guía de prácticas clínicas para el diagnóstico y tratamiento de ATR en pacientes pediátricos”, con un alcance de 15,641 personas (https://bit.ly/2MbuxMq).
3. “Los dos primeros años de vida son críticos para el crecimiento de los niños”, con un alcance de 12,352 personas (https://bit.ly/2nDW62h).

Los videos publicados en Facebook que han sido más consultados son:

1. “Acidosis Tubular Renal (material original)”, con un alcance de 3,355 personas en el canal de la FUNATIM.
2. “Córdoba realiza el primer trasplante de hígado entre una abuela y su nieto”, con un alcance de 2,685 personas.
3. “Testigo daño renal infantil, entrevista a la Dra. Laura Escobar para el programa ‘Creadores Universitarios’ por Foro TV”, con un alcance de 1,629 personas.

Canal de YouTube

El canal de FUNATIM SIPSE en YouTube fue creado el 23 de abril de 2015. Desde su inicio hasta el 27 de enero de 2018, la gestión del canal ha acumulado 635 suscriptores y 87 videos publicados, los cuales han sido visualizados 86,617 veces y compartidos 1,074 veces. Respecto a la retención de la audiencia, un usuario promedio del canal visualiza 5 minutos 49 segundos de material producido por el canal de la FUNATIM. Al igual que los demográficos del sitio web y la página de fans de Facebook, la mayoría de la audiencia del canal de la FUNATIM es del género femenino (58%) de 25 a 34 años, pero los hombres de la misma edad son los que más tiempo permanecen en el canal. Los usuarios que han consultado los videos de la FUNATIM provienen principalmente de Latinoamérica: México (39%), Perú (11%), Colombia (9.4%), Argentina (8.4%), Venezuela (4.9%) y Chile (4.4%). De esta muestra, 95% ha consultado los videos a través de la plataforma youtube.com y sólo 5% a través de otros sitios externos donde se han insertado los videos. La mayoría de los usuarios (50%) que han visualizado los videos del canal ha sido porque los contenidos les han aparecido como “videos relacionados”. La segunda fuente de tráfico a los contenidos ha sido a partir del uso del buscador de YouTube (24%), lo cual indica que los contenidos cuentan con el etiquetado suficiente para ser encontrados con facilidad a través de la plataforma de Youtube.

El contenido publicado en el canal de Youtube pasa por un proceso de curaduría, con la intención de presentar contenidos de calidad para la comunidad interesada. Los materiales se componen de animaciones, conferencias y grabaciones de eventos organizados por la propia Fundación. Los usuarios del canal consumen en promedio 22% de la duración total de los vídeos publicados por la FUNATIM en YouTube. Cabe destacar que la mayoría de los videos publicados tienen una duración mayor a 30 minutos. Si se considera que el tema tratado es especializado y que los consumidores promedio prefieren consultar vídeos de corta duración en Youtube, es relevante que los usuarios pasen en promedio 5.49 minutos visualizando el contenido.

Con base en la lista de los videos con mayor número de visualizaciones y su asociación a la cantidad de Me gusta (635) y No me gusta (38), se puede concluir que el contenido es aceptado positivamente por la comunidad. El canal de la FUNATIM ha recibido un total de 50 comentarios, de los cuales 10 han sido asociados a un vídeo que explica el caso de un niño que sufrió las consecuencias de un falso diagnóstico de ATR. Este video es uno de los de menor duración (3.58 min) en el canal.

Posterior a la publicación del sitio web, y la actividad que se ha ido generando en los canales de la FUNATIM, han surgido comunidades activas que fomentan la difusión y participación del público interesado, entre las que destacan el grupo privado: “Creciendo juntos (Acidosis Tubular Renal)” con una comunidad de 1,175 miembros y el grupo público de “Acidosis Tubular Renal (El diagnóstico infundado)” con 751 miembros. Ambas comunidades, surgieron por madres de niños atendidos por la FUNATIM y que, en busca de continuar con la labor de difusión y prevenir los casos de falsos diagnósticos, brindan apoyo y asesoría a padres de niños a los que les han diagnosticado ATR. Al analizar el tipo de contenido compartido en estos grupos, se identificó que en su mayoría son testimonios de la propia comunidad, donde también se comparten materiales informativos, eventos y contenidos generados por la FUNATIM.

Conclusiones

Los canales digitales gestionados con responsabilidad son una fuente de conocimiento y experiencias que puede almacenarse para informar atemporalmente a la población, independientemente de que el tema tratado sea sumamente especializado y afecte solo a un reducido sector de la población.

El sitio de la FUNATIM se encuentra posicionado en los principales motores de búsqueda, al realizar consultas con el término “Acidosis Tubular Renal”. Asimismo, el sitio ha sido fuente de referencia a través de revistas, boletines de la SIPSE, así como blogs y sitios web externos.

Las redes sociales permiten convocar a personas y formar comunidades sólidas que se mantienen informadas, se identifican y apoyan entre sí. Las redes sociales que ayudaron a la difusión de la labor de la FUNATIM tuvieron la capacidad de lograr acuerdos con la Secretaría de Salud, principal órgano gubernamental, para elaborar la “Guía de prácticas clínicas para el diagnóstico y tratamiento de la ATR en pacientes pediátricos”.

Referencias

• Acidosis tubular renal (El diagnóstico infundado). Disponible en: https://www.facebook.com/groups/594369127252927/?fref=ts.
• Blog Acidosis Tubular Renal – ATR (enero, 2012). http://atr-acidosistubularrenal.blogspot.mx.
• Boletín UNAM-DGCS-514 (31 agosto, 2011). Consultado el 11 de agosto 2018. Disponible en: http://www.dgcs.unam.mx/boletin/bdboletin/2011_514.html.
• Carrisoza-Gaytán, R., Rangel, C., Saldaña-Meyer, R., Salvador, C., Escalona, C., Satlin, L. M., et al. The hyperpolarization-activated cyclic nucleotide-gated HCN2 channel transports ammonium in the distal nephron. Kidney Int 2011; 80:832-40. https://doi.org/10.1038/ki.2011.230.
• CENETEC. Diagnóstico y Tratamiento de la Acidosis Tubular Renal en pacientes pediátricos. Guía de Evidencias y recomendaciones, México, Centro Nacional de Excelencia Tecnológica en Salud, Secretaria de Salud; 2016 (consulta 11 de agosto 2018). Disponible en: http://cenetec-difusion.com/CMGPC/SS-255-16/ER.pdf.
• Creciendo juntos acidosis tubular renal. Disponible en: https://www.facebook.com/groups/creciendojuntosatr/?fref=ts.
• Devuyst, O., Knoers, NVAM, Remuzzi, G. y Schaefer, F. (2014). Rare inherited kidney diseases: challenges, opportunities and perspectives. Lancet; 383:1844-1859. https://doi.org/10.1016/S0140-6736(14)60659-0.
• Elhayek, D., Perez de Nanclares, G., Chouchane, S., Hamani, S., Mlika, A., Troudi, M., et al. (2013). Molecular diagnosis of distal renal tubular acidosis in Tunisian patients: proposed algorithm for Northern Africa populations for the ATP6V1B1, ATP6V0A4 and SCL4A1 genes. BMC Med Genet; 14:119. DOI: https://doi.org/10.1186/1471-2350-14-119.
• Escobar-Pérez, L. I., Mejía, N., Gil, H. y Santos, F. (2013). La acidosis tubular renal distal (ATRD): una enfermedad hereditaria rara en la que no se puede eliminar la carga ácida. Nefrología 33:289-96. DOI: https://doi.org/10.3265/Nefrologia.pre2012.Oct.11592.
• FEDER (2009). Estudio sobre situación de necesidades socio sanitarias de las personas con enfermedades raras en España. Estudio ENSERio [edición electrónica] https://enfermedades-raras.org/images/stories/documentos/Estudio_ENSERio.pdf.
• Gil-Peña, H., Mejía, N. y Santos, F. (2014). Renal tubular acidosis. J Pediatr ;164: 691-98. DOI: https://doi.org/10.1016/j.jpeds.2013.10.085.
• Gómez, J., Gil-Peña, H., Santos, F., Coto, E., Arango, A., Hernández, O., et al. (2016). Primary distal renal tubular acidosis: novel findings in patients studied by next-generation sequencing. Pediatric Research; 79: 496-501. DOI: https://doi.org/10.1038/pr.2015.243.
• Gomez-Salas, D. (2011). Detección y detención de los daños de la acidosis tubular renal. Consultado el 11 de agosto 2018. http://blogs.monografias.com/noticiencias/2011/09/01/deteccion-y-detencion-de-los-danos-de-la-acidosis-tubular-renal/.
• Guerra-Hernandez, N., Matos-Martínez, M., Ordaz-López, K., Camargo-Muñiz, D., Medeiros, M., Escobar-Pérez, L. (2014). Clinical features and progress of mexican patients with distal renal tubular acidosis. Rev Invest Clin 2014; 66(5)386-392. http://www.medigraphic.com/pdfs/revinvcli/nn-2014/nn145b.pdf.
• Muñoz-Arizpe, R., Escobar, L., Medeiros, M. (2012). Over-diagnosis of renal tubular acidosis in Mexico. Rev Invest Clin; 64:399-401. http://www.medigraphic.com/pdfs/revinvcli/nn-2012/nn124j.pdf.
• Muñoz-Porras, V. (2011). Enfermedades de moda y su sobre diagnóstico. Consultado el 9 de agosto 2018. Disponible en: http://www.mama-freelance.com/2011/05/06/enfermedades-de-moda-y-su-sobre-diagnstico-el-caso-particular-del-atr/.
• Soliman, N. A. (2012). Orphan kidney diseases. Nephron Clin Pract; 120: c194-9. DOI: https://doi.org/10.1159/000339785.
• Stover, E. H., Borthwick, K. J., Bavalia, C., Eady, N., Fritz, D. M., Rungroj, N., et al. (2002). Novel ATP6V1B1 and ATP6V0A4 mutations in autosomal recessive distal renal tubular acidosis with new evidence for hearing loss. J Med Genet; 39: 796-803. https://jmg.bmj.com/content/39/11/796.
• Valdéz, B. (2012). Alertan de fraude con rara enfermedad (29 noviembre, 2012). https://sipse.com/ciencia-y-salud/alertan-de-fraude-con-rara-enfermedad-3064.html.
• Yañez, G. (2013). Petición change.org. Secretaria de Salud México: Instaurar un protocolo oficial para el correcto diagnóstico de la “ATR”. Consultado el 11 de agosto 2018. https://bit.ly/2MGzpFj.

Agradecimiento: a la Cátedra Especial Doctor Bernardo Sepúlveda Gutiérrez que me otorgó la Facultad de Medicina, UNAM, para hacer este trabajo.

Recepción: 6/3/2018. Aprobación: 8/8/2018.