Definición
de fractal
Como
anteriormente se ha insinuado, la aparición
propiamente tal de los fractales coincide
con la edición de Les objets
fractals: Forme, hasard et dimension,
en 1975 y reeditado en 1977. En esta obra,
Mandelbrot realiza una serie de definiciones
en torno a los fractales.
En
1982, el mismo Mandelbrot publica un nuevo
libro, con gráficos sorprendentes
creados con la tecnología informática
que, por aquel tiempo, estaba a su disposición.
Este libro se llama, The Fractal Geometry
of Nature. En esta obra, Mandelbrot
(1982/1997) propone otra
definición.
El autor acuña el término
fractal para acoger a los distintos “monstruos”
matemáticos que progresivamente fueron
aumentando en cantidad, acompañados
por aquellos “monstruos” que
se fueron descubriendo en la naturaleza.
La palabra fractal deriva del adjetivo latino
fractus, que significa fragmentado, quebrado
o irregular, lo que corresponde exactamente
con las características gráficas
de los objetos fractales y con su respectiva
dimensión.
La
dimensión fractal se puede definir
matemáticamente como:
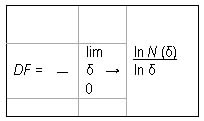
en donde N (d) es el número de elementos
de longitud característica d necesarios
para recubrir el conjunto estudiado.
Sin
embargo, se está ante un concepto
geométrico para el que aún
no existe una definición precisa,
ni una teoría única y comúnmente
aceptada, razón por la cual es difícil
encontrar una definición satisfactoria
del concepto fractal. No obstante, se pueden
extraer algunas características fundamentales
que, de cumplirse una o todas, se podría
hablar de un conjunto fractal. Así,
un
conjunto fractal sería
(Mas, Mach, Trigueros, Claret & Sagués,
1996):
Existen,
además, algunas características
adicionales propias de las estructuras fractales.
De este modo, una estructura fractal satisface
alguna(s) de las
propiedades siguientes
(Falconer, 1990).
Intentando
integrar los aspectos que tienen más
relevancia en una gran cantidad de definiciones,
se propone la siguiente definición:
Los
fractales son formas (o bien que se encuentran
en la naturaleza, o bien creadas matemáticamente,
o bien derivadas de la caracterización
gráfica del comportamiento de un
sistema), que poseen una irregularidad,
expresada en una dimensionalidad no entera,
que se mantiene y que es característica
a distintas escalas de análisis,
cumpliendo así con una de sus cualidades
más notables, la autoafinidad, que
significa que la parte es semejante al todo.
Teniendo
ya una definición con la cual se
pueda identificar a un objeto fractal, se
puede analizar su característica
fundamental, a saber, la autosimilitud (self-
similarity). Se dice que una estructura
es autosimilar si puede ser cortada arbitrariamente
en trozos pequeños, cada uno de los
cuales es una pequeña réplica
de la estructura completa (Peitgen, Jürgens
& Saupe, 1992). En estricto rigor, el
concepto de autosemejanza o autosimilitud
se aplica sólo en fractales matemáticos
(que surgen de la iteración de fórmulas
sencillas pero que llevan a estructuras
muy complejas. e.g. Polvo de Cantor, Curva
de Peano, Copo de Nieve de Koch, etc.),
mientras que en los fractales naturales
o físicos (aquellos que se encuentran
en la naturaleza. e.g. una hoja de helecho,
una arborización bronquial, os capilares
sanguíneos, etc.) se aplica el concepto
de autoafinidad, ya que su fractalidad es
solamente estadística y poseen, en
consecuencia, un escalamiento anisotrópico
(que no tiene las mismas propiedades en
todas dimensiones de análisis), lo
que no permite que una parte amplificada
de una figura mantenga exactamente las características
de la figura como un todo (Hinojosa &
Chávez, 2001).
Resulta
interesante notar que la irregularidad de
los objetos fractales pasa a ser una característica
particular del objeto y da cuenta de la
similitud que tienen sus partes respecto
al todo, con independencia de la escala
de análisis utilizada, condición
que gráficamente se puede observar
en la Figura 5.