Axiomas
de orden
II.1 Si el punto C está entre A y
B, entonces A, B y C están en una misma línea,
C está entre B y A, B no está entre A
y C, y A no está entre B y C.
![]()
II.2 Si A y B son dos puntos distintos dados, hay un punto C que está entre A y B, y un punto D tal que B está entre A y D.
![]()
II.3 Si A, B y C son tres puntos distintos en
una misma línea, entonces uno de ellos está entre los otros
dos.
Definiciones. Por el segmento AB se entiende
los puntos A y B y todos los que están entre A y B.
Los puntos A y B se llaman extremos del segmento. Un
punto C se dice que está sobre el segmento si
es alguno de sus extremos o está entre A y B.
Definición. Dos líneas, una línea
y un segmento, o dos segmentos, se dice que se cortan si hay
un punto que está en ambos.
Definición. Sean A, B y C tres puntos
que no están en una misma línea. Por el triángulo
ABC se entiende los tres segmentos AB, BC y CA. Se dice que estos
segmentos son los lados del triángulo, y los puntos A,
B y C se llaman vértices del triángulo.
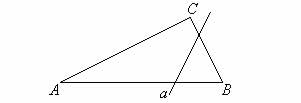
II.4 (Postulado de Pasch) Una línea que corta
un lado de un triángulo y que no pasa por ninguno de sus vértices
deberá cortar también otro lado del triángulo.20
Respecto al lenguaje, Hilbert podría haber escrito las proposiciones geométricas en la notación simbólica desarrollada por Peano y su escuela para la teoría de la cuantificación, pero no lo quiso hacer. Por ejemplo, en vez del enunciado “los puntos A y B están en la recta a” pudo escribir simplemente f(A, B, a), de modo que la expresión misma no contuviera referencias a ninguna relación intuitiva. Una fórmula como f(A, B, a) representa en general una relación entre ternas de objetos, de la que lo único que sabríamos sería lo que especificaran los axiomas. No obstante, Hilbert prefirió no recurrir a un simbolismo de esta naturaleza para atraer un mayor número de matemáticos.
En
cuanto al planteamiento de la teoría, esta es la idea subyacente:
de sus objetos nada sabemos de antemano; más bien, éstos,
junto con sus mutuas relaciones, quedan definidos de manera implícita
por medio de los axiomas. El significado que pudieran tener sus términos
es irrelevante para el desarrollo de la teoría, pues en su despliegue
sólo se habrá de apelar a la lógica y los axiomas.
Si alguien preguntara “¿qué son los puntos?”,
“¿qué son las líneas?” la única
respuesta sería “cualquier sistema de objetos y relaciones
entre ellos que satisfaga estos axiomas” y se le mostraría
la lista de estos últimos.21