|
El método de Hartree-Fock
Dentro de la aproximación de núcleos fijos existen
varias vertientes para obtener una estimación de la función de
onda. Una de ellas es modelar directamente a la función de onda.
En un inicio se propuso a esta función como el producto de orbitales,
un orbital por cada electrón. Sin embargo, se sabe que la función
de onda verdadera debe de cambiar de signo cuando las coordenadas
entre dos electrones se intercambian, se le conoce a este hecho
como principio de antisimetría, y es un reflejo del comportamiento
que deben de exhibir los electrones.9 Con
esta restricción en 1929 John C. Slater propuso como expresión
general de la función de onda a un determinante constituido por
orbitales, en vez de un simple producto entre ellos.11 En
términos esquemáticos tenemos que
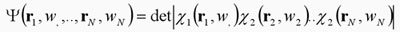 |
(2) |
En esta ecuación hemos remarcado el hecho de que
el electrón 1 tiene como coordenadas a r1=x1,
y1, z1, por la parte
espacial, y una variable de espín, w1. Para N electrones
tendremos 4N coordenadas. Por cada electrón se propone
dentro del determinante una función, un orbital, y por lo tanto
el determinante será de tamaño N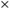 N. El problema
ahora es determinar los orbitales, las funciones, que deben de
ser incluidos en el determinante. Afortunadamente la función de
onda tiene asociado un principio variacional, donde se sabe que
la función de onda del sistema será aquella que minimice a la energía,
en otras palabras, la función de onda debe de minimizar a N. El problema
ahora es determinar los orbitales, las funciones, que deben de
ser incluidos en el determinante. Afortunadamente la función de
onda tiene asociado un principio variacional, donde se sabe que
la función de onda del sistema será aquella que minimice a la energía,
en otras palabras, la función de onda debe de minimizar a
 |
(3) |
Como en la ecuación 2 se ha escrito a la función
de onda en términos de orbitales entonces la minimización de la
energía debe de ser con respecto a los orbitales. Cuando tenemos
en cálculo diferencial el problema de minimización con respecto
a una variable resulta que para encontrar el mínimo, después de
igualar la derivada a cero, debemos de encontrar las raíces de
una función, en el mejor de los casos un polinomio. En el caso
de la minimización de la ecuación 3 lo que obtenemos es una ecuación
diferencial en lugar del polinomio y en lugar de la búsqueda de
raíces se busca a las funciones que satisfacen la ecuación diferencial
 |
(4) |
Podemos darnos cuenta que esta ecuación se parece
mucho a la ecuación 1. Sin embargo, existen dos diferencias fundamentales
entre ellas. 1) La ecuación 4 está asociada a un orbital, así se
ha transformado el problema de resolver una ecuación que depende
de N partículas a N problemas que dependen de las coordenadas de
una partícula. 2) El operador  de
la ecuación 1 se conoce exactamente al saber las interacciones
que existen dentro de una molécula lo cual no es cierto para el
operador de
la ecuación 1 se conoce exactamente al saber las interacciones
que existen dentro de una molécula lo cual no es cierto para el
operador 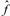 ya
que este operador contiene partes que se escriben en términos de
los orbitales. ¿Cómo encontrar a los orbitales si no conocemos
el operador con el que los vamos a obtener? La forma en que se
procede para resolver este problema es proponer un operador de
prueba, con este operador de inicio se obtiene un conjunto de orbitales,
con estos orbitales construimos nuevamente al operador ya
que este operador contiene partes que se escriben en términos de
los orbitales. ¿Cómo encontrar a los orbitales si no conocemos
el operador con el que los vamos a obtener? La forma en que se
procede para resolver este problema es proponer un operador de
prueba, con este operador de inicio se obtiene un conjunto de orbitales,
con estos orbitales construimos nuevamente al operador 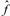 y así sucesivamente.
Este proceso iterativo se termina cuando decidimos que la energía
del sistema es lo suficientemente parecida a la iteración previa
o que el potencial entre una iteración y otra no cambia sustancialmente.
Hemos descrito muy brevemente el método conocido como Hartree-Fock,
el cual es un pilar en los métodos de la química cuántica computacional
hoy en día, tanto por sus ideas como por la manera en que se resuelve
la ecuación 4. y así sucesivamente.
Este proceso iterativo se termina cuando decidimos que la energía
del sistema es lo suficientemente parecida a la iteración previa
o que el potencial entre una iteración y otra no cambia sustancialmente.
Hemos descrito muy brevemente el método conocido como Hartree-Fock,
el cual es un pilar en los métodos de la química cuántica computacional
hoy en día, tanto por sus ideas como por la manera en que se resuelve
la ecuación 4.
La solución de la ecuación 4 es todo un reto, primeramente
lo que se hace es imponer la variable de espín en cada orbital.
Esto es muy importante ya que esto determina el espín total del
sistema. Para el espín solamente tenemos dos posibilidades ya que
puede tener el valor de ½ o –½ y esto nos lleva a poder escribir
a cada orbital como el producto de dos funciones, una que depende
de la parte espacial, 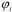 ,
y otra de la parte de espín, ,
y otra de la parte de espín, 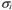 , esto es . , esto es .
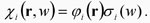 |
(5) |
Evidentemente, dependiendo del espín que tenga
asociado cada orbita el sistema podrá tener un espín neto de 0,
½, 1, 3/2, ... Lo cual define si el sistema se encuentra en un
sigulete, doblete,
triplete, etcétera.
9. Levine, I. N. Quantum
Chemistry, 6th
Economy Edition. Prentice Hall India, 2008.
11. Slater,
J. C. Phys.
Rev. (1929) 34,
1293.
|






