|
La necesidad de una computadora
Para la solución de la ecuación 4, teniendo en cuenta
la ecuación 5, Clemens C. J. Roothaan.12 y
George G. Hall13 hicieron
de manera independiente una propuesta muy sencilla para poder ser
implementada en sistemas moleculares, basándose en el método de
Ritz. Es importante mencionar que este proceder es lo que hoy domina
el mundo de la química cuántica computacional. La idea es muy sencilla
ya que cada orbital se representa en términos de un conjunto de
funciones conocidas. Supongamos que se propone al conjunto de funciones
{fk(r) con k = 1,2,..,K}, entonces cada orbital i será
representado por la combinación lineal de estas funciones
de base de la siguiente manera .
Como las funciones fk son conocidas entonces
lo que ahora se necesita buscar es el conjunto de coeficientes 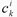 .
Nótese que basta un conjunto de funciones de base ya que el conjunto
de .
Nótese que basta un conjunto de funciones de base ya que el conjunto
de 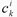 será diferente
para cada orbital. Al sustituir la ecuación 6 en 5 y ésta en 4
se obtiene un problema algebraico para los coefcientes será diferente
para cada orbital. Al sustituir la ecuación 6 en 5 y ésta en 4
se obtiene un problema algebraico para los coefcientes 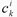 con
la siguiente forma con
la siguiente forma
En esta ecuación cada una de las cantidades representa
una matriz, un arreglo de K K elementos. Al tener un operador de inicio, en nuestro proceso iterativo,
la matriz F se conoce y tiene varias contribuciones, todos sus
elementos son el resultado de evaluar integrales: la contribución
de la energía cinética de los electrones, la interacción electrostática
núcleo-electrón y electrón-electrón. Además aparece un término
adicional que surge como consecuencia de escribir a la función
de onda como un determinante, para que la función de onda sea antisimétrica.
A este término adicional a la energía se le conoce como energía
de intercambio. La matriz
S está compuesta de integrales del producto entre las mismas funciones
de base K elementos. Al tener un operador de inicio, en nuestro proceso iterativo,
la matriz F se conoce y tiene varias contribuciones, todos sus
elementos son el resultado de evaluar integrales: la contribución
de la energía cinética de los electrones, la interacción electrostática
núcleo-electrón y electrón-electrón. Además aparece un término
adicional que surge como consecuencia de escribir a la función
de onda como un determinante, para que la función de onda sea antisimétrica.
A este término adicional a la energía se le conoce como energía
de intercambio. La matriz
S está compuesta de integrales del producto entre las mismas funciones
de base
Para la construcción de una parte de la matriz
F es necesario evaluar integrales que se conocen como integrales
bielectrónicas y que son de la forma
Son precisamente estas integrales las que son un
cuello de botella en el uso del método de Hartree-Fock. Pensemos
en que usamos 10 funciones de base para estudiar a la molécula
de agua con el método de Hartree-Fock. En este caso se tendría
que evaluar 100 integrales (10 10) para la matriz S.
Claro, se puede ver que hay simetría en algunas integrales y no
se tendrán que evaluar todas ya que Sij=Sji.
En realidad cuando se tiene integrales entre dos funciones de base
no se tendrá problema alguno. Sin embargo, pensemos en el mismo
caso para las integrales bielectrónicas, con ellas se tendrán que
evaluar 10000 integrales (10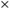 10 10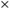 10 10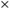 10).
También es cierto que para estas integrales se tiene simetría y
hay que evaluar del orden K4/8 integrales. En estos
días, para el estudio de un sistema de interés farmacéutico como
la 10).
También es cierto que para estas integrales se tiene simetría y
hay que evaluar del orden K4/8 integrales. En estos
días, para el estudio de un sistema de interés farmacéutico como
la 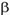 -ciclodextrina
se requieren del orden de 1800 funciones de base. Eso significa
que tendremos matrices de un tamaño de 1800 -ciclodextrina
se requieren del orden de 1800 funciones de base. Eso significa
que tendremos matrices de un tamaño de 1800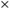 1800
(3240000 elementos) y alrededor de 1.3122 1012 integrales bielectrónicas
que evaluar. De aquí es claro que es necesario el uso de una computadora. 1800
(3240000 elementos) y alrededor de 1.3122 1012 integrales bielectrónicas
que evaluar. De aquí es claro que es necesario el uso de una computadora.
12. Roothaan,
C. C. J. Rev. Mod. Phys. (1951) 23,
69.
13. Hall, G. G. Proc.
Royal Soc. London A (1951) 205,
541.
| 





